Let’s consider a Hidden Markov Model describing a sequential problem: a system has three internal (hidden) states:

• Ok (Everything works correctly)
• Some issues (not blocking)
• Out of order

However, we can observe only a sensor (globally connected with different sub-systems) which states are represented by three colors (green, yellow and red), representing respectively a normal, partially dangerous and absolutely risky situation. They are directly connected with a precise component, so we don’t know if there’s a failure or a false-positive (sometimes another sensor can fail). We can observe this sequence and try to predict the internal states. That’s what you can achieve with HMM. I cannot expose all the theory behind them however you can find some good references at the end of this post. This is a graphical representation of such a process (only 5 time-steps).

A prediction can be achieved using an algorithm called “Fixed-delay Smoothing” which combines forward propagation of messages (conditional probabilities of internal states given all sensor data received till a specific time-step) and backward smoothing (past conditional probability tuning). This Python snippet shows how to simulate the process described above:

The result of a simulation example (with all values declared in the snippet) is:

HMM simulation
Log example
O2: Yellow -> Some issues (76.553%)
O3: Red -> Out of order (61.044%)
O4: Green -> Ok (70.410%)
O5: Red -> Out of order (55.231%)
O6: Yellow -> Some issues (78.504%)
O7: Yellow -> Some issues (77.122%)
O8: Red -> Out of order (60.867%)
O9: Yellow -> Some issues (79.078%)
O10: Green -> Ok (81.680%)
O11: Yellow -> Some issues (69.912%)
O12: Green -> Ok (84.343%)
O13: Green -> Ok (89.372%)
O14: Yellow -> Some issues (69.000%)
O15: Green -> Ok (84.513%)
O16: Green -> Ok (89.387%)
O17: Yellow -> Some issues (68.998%)
O18: Green -> Ok (84.514%)
O19: Green -> Ok (89.387%)
O20: Yellow -> Some issues (68.998%)
O21: Green -> Ok (84.514%)
O22: Green -> Ok (89.387%)
O23: Red -> Out of order (48.530%)
O24: Yellow -> Some issues (77.950%)
O25: Yellow -> Some issues (76.991%)
O26: Red -> Out of order (60.815%)
O27: Green -> Ok (70.758%)
O28: Green -> Ok (87.973%)
O29: Green -> Ok (89.669%)
O30: Green -> Ok (89.816%)
O31: Green -> Ok (89.829%)
O32: Yellow -> Some issues (68.944%)
O33: Yellow -> Some issues (75.429%)
O34: Yellow -> Some issues (76.240%)
O35: Green -> Ok (83.310%)
O36: Green -> Ok (89.282%)
O37: Red -> Out of order (48.568%)
O38: Yellow -> Some issues (77.954%)
O39: Green -> Ok (82.139%)
O40: Red -> Out of order (50.895%)
O41: Red -> Out of order (73.598%)
O42: Red -> Out of order (77.923%)
O43: Green -> Ok (62.732%)
O44: Red -> Out of order (57.583%)
O45: Yellow -> Some issues (78.695%)
O46: Red -> Out of order (62.948%)
O47: Yellow -> Some issues (79.229%)
O48: Yellow -> Some issues (77.280%)
O49: Red -> Out of order (60.928%)

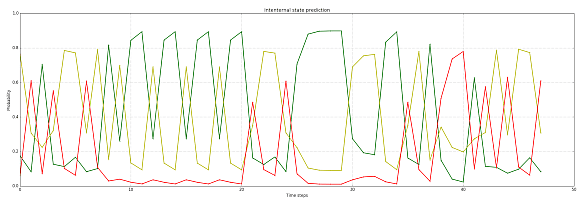
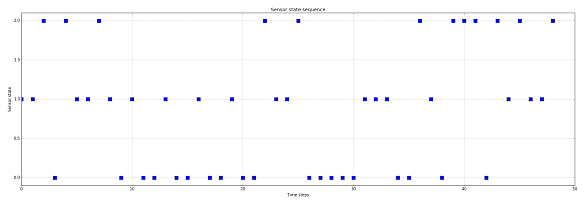
You can notice that a sequence of equal states (confirmed) increases the probability of an internal state, while an abrupt change is not considered immediately with the highest probability. These sequences can be also represented with these plots which show respectively the sequence of sensor states (low = green, medium = yellow, high = red) and the probabilities of each internal state:

Reference:

• Russel S., Norvig P., Artificial Intelligence: a modern approach, Pearson (Amazon)
• Wikipedia page about HMM

See also:

Machine Learning Algorithms – Giuseppe Bonaccorso

My latest machine learning book has been published and will be available during the last week of July. From the back cover: In this book you will learn all the important Machine Learning algorithms that are commonly used in the field of data science.