The Hodgkin-Huxley model (published on 1952 in The Journal of Physiology [1]) is the most famous spiking neuron model (also if there are simpler alternatives like the “Integrate-and-fire” model which performs quite well). It’s made up of a system of four ordinary differential equations that can be easily integrated using several different tools. The main idea is based on an electrical representation of the neuron, considering only Potassium (K) and Sodium (Na) voltage-gated ion channels (even if it can be extended to include more channels). A schematic representation is shown in the following figure:
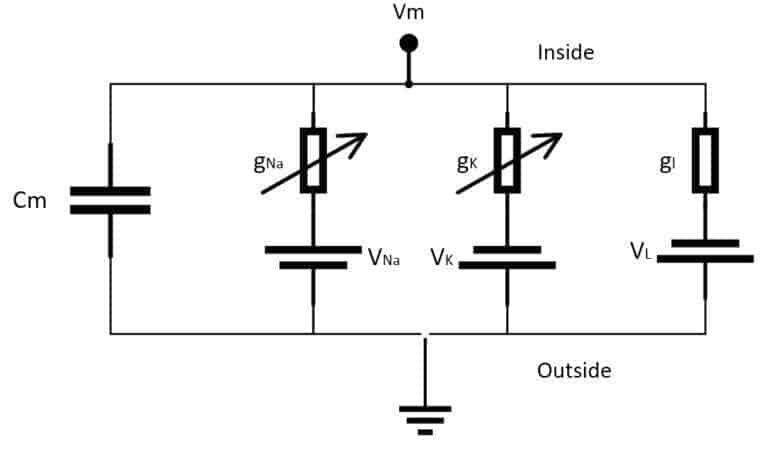
The elements are:
- Cm: a capacitance per unit area representing the membrane lipid-bilayer (adopted value: 1 µF/cm²)
- gNa: voltage-controlled conductance per unit area associated with the Sodium (Na) ion-channel (adopted value: 120 µS/cm²)
- gK: voltage-controlled conductance per unit area associated with the Potassium (K) ion-channel (adopted value: 36 µS/cm²)
- gl: conductance per unit area associated with the leak channels (adopted value: 0.3 36 µS/cm²)
- VNa: voltage source representing the electrochemical gradient for Sodium ions (adopted value: 115 mV)
- VK: voltage source representing the electrochemical gradient for Potassium ions (adopted value: -12 mV)
- Vl: voltage source that determines the leakage current density together with gl (adopted value: 10.613 mV)
In the scheme, the external stimulus current is not shown, however, we assume its presence as a current density (I) encoding the input signal. All the experimental values are the same proposed by the authors in [1] and refer to an equilibrium potential of 0 V. The system is defined through the following ODE system:
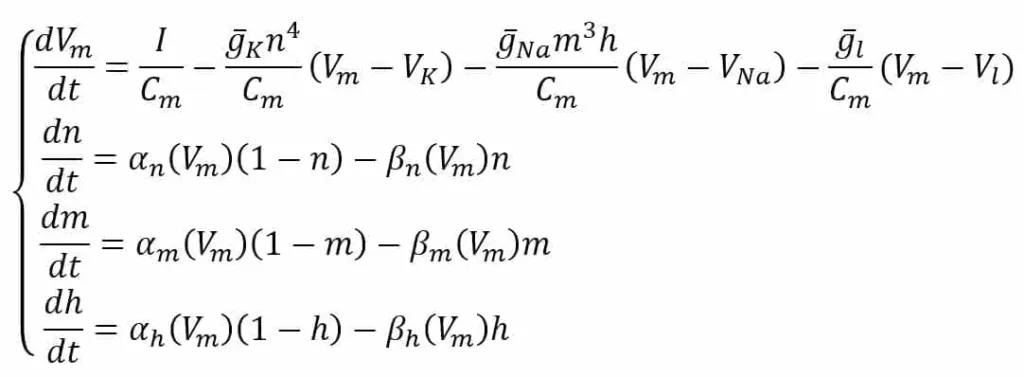
The first equation defines the derivative of Vm considering the external stimulus (I) and the contribution of K, Na, and leakage current densities. The variables n, m, and h are associated with the probability of each channel to open and they are strictly dependent on the nature of the channel. For example, the K channel is voltage-gated and has four sub-units that must be all open in order to allow the current to flow, therefore its probability is n to the power of 4. Sodium has a slightly more complex behavior and needs two different factors (m and h) with autonomous dynamics. The last three equations describe the ion-channel kinetic model by computing the derivatives of n, m, and h as functions of the same variables and two voltage-dependent functions. The first term is the number of closed channels that are opening, while the second term is the number of open channels that are closing.
Hodgkin and Huxley suggest the following functions:
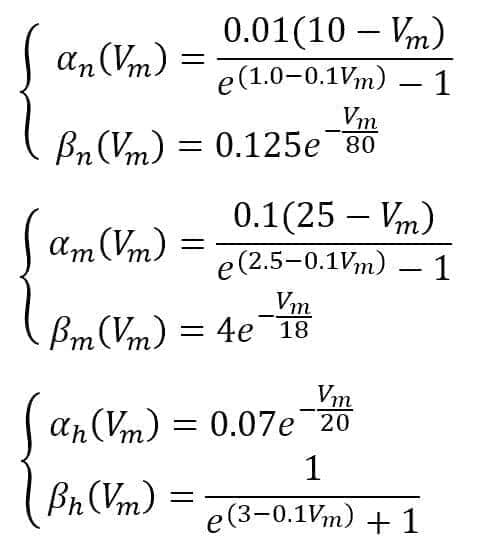
In the simulation, we’re going to use a double-impulsive current density as stimulus (however, any other signal can be used to test different behaviors). The time range is [0, 50ms]:
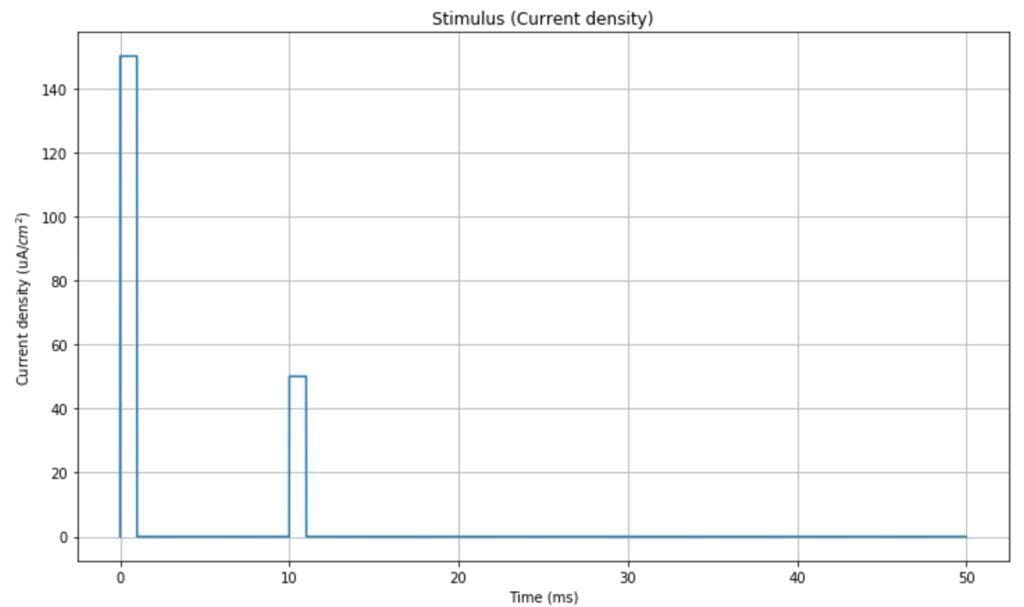
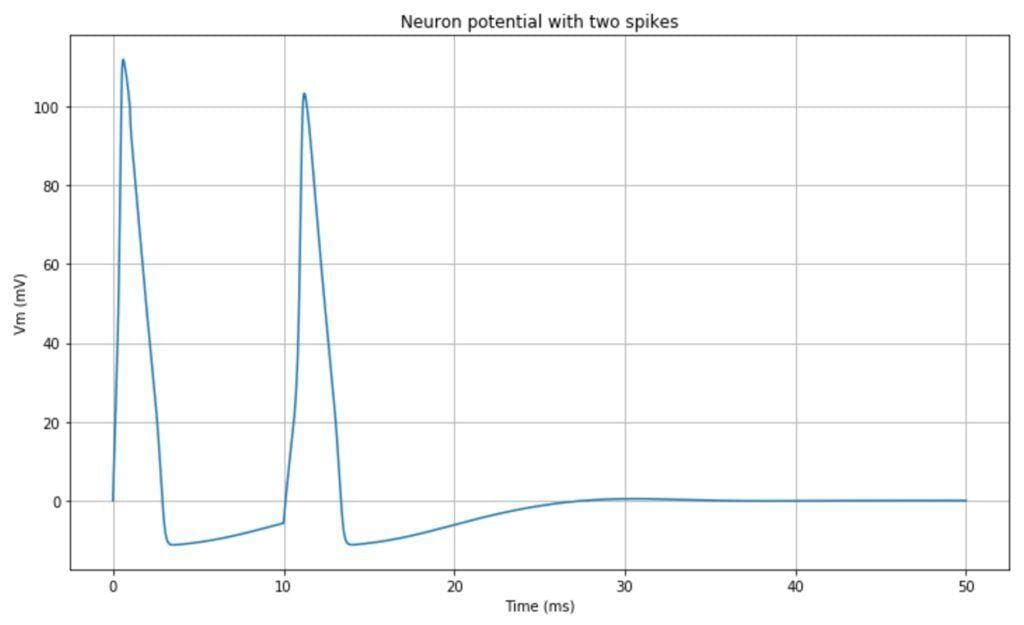
The resulting impulsive neuron behavior is shown in the following plot:
It’s also possible to observe the limit cycles present in the dynamic system. In the following plot, the trajectories Vm – n, and Vm – m are plotted:
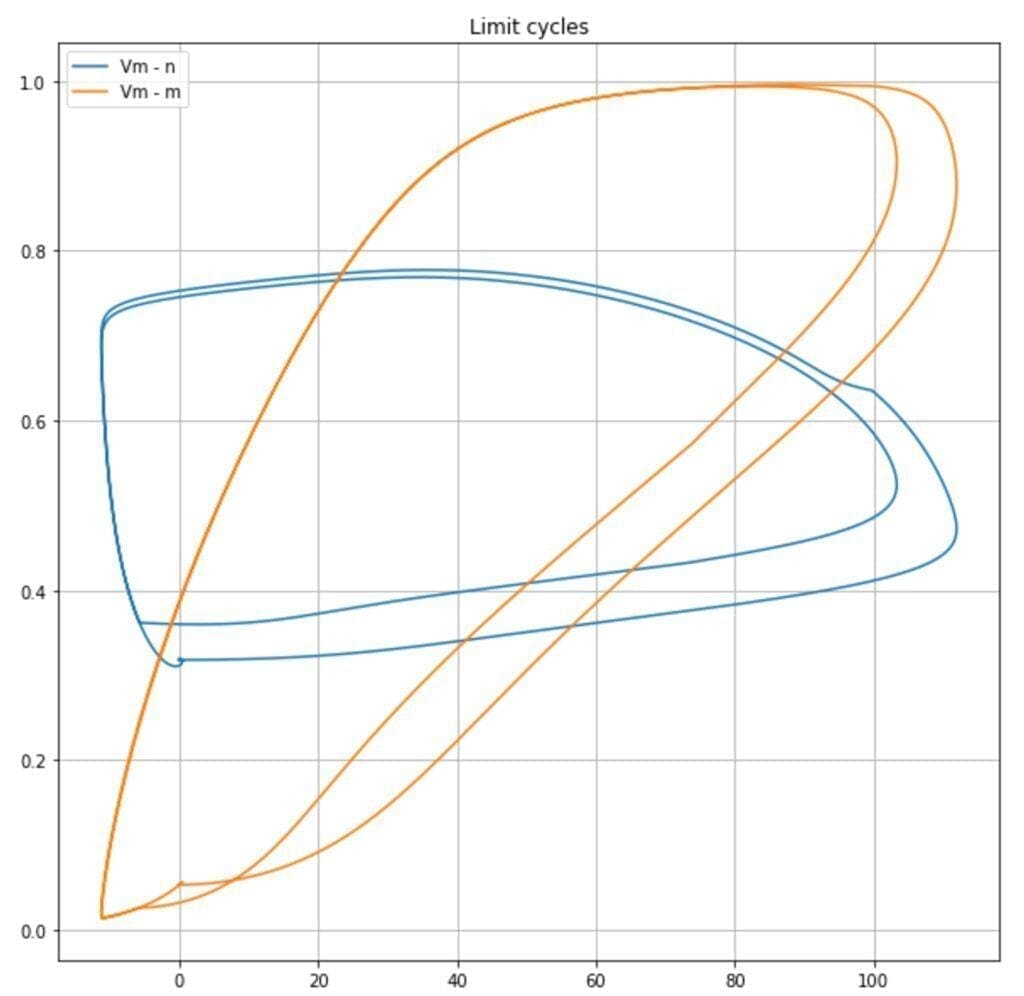
It’s possible to observe how the probabilities (proportional to n, m, and h) for ion-channels to be opened span from a minimum to a maximum value according to n and Vm in a cyclic fashion. This allows the oscillations: steady state, potential increase, spike, potential decrease, steady state.
The complete Python code is available in this GIST:
References:
- Hodgkin, A. L., Huxley, A. F., (1952), A quantitative description of membrane current and its application to conduction and excitation in nerve. The Journal of Physiology, 117 doi: 10.1113/jphysiol.1952.sp004764
- Abbott L. F., Dayan P., Theoretical Neuroscience: Computational and Mathematical Modeling of Neural Systems, The MIT Press
See also:
ML Algorithms Addendum: Hebbian Learning – Giuseppe Bonaccorso
Hebbian Learning is one the most famous learning theories, proposed by the Canadian psychologist Donald Hebb in 1949, many years before his results were confirmed through neuroscientific experiments.