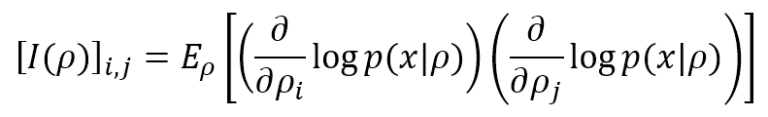Fisher Information, named after the statistician Ronald Fisher, is a very powerful tool in both Bayesian Statistics and Machine Learning. To understand its “philosophical” meaning, it’s useful to think about a simple classification task, where our task is to find a model (characterized by a set of parameters) that is able to reproduce the data generating process p(x) (normally represented as a data set) with the highest possible accuracy. This condition can be expressed using the Kullback-Leibler divergence:

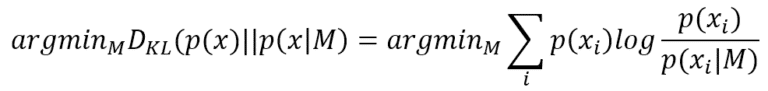
Finding the best parameters that minimize the Kullback-Leibler divergence is equivalent to maximizing the log-likelihood log P(x|M) because p(x) doesn’t contain any reference to M. Now, a good (informal) question is: how much information p(x) can provide to simplify the task to the model? In other words, given a log-likelihood, which is its behavior next to the MLE point?

Considering the following two plots, we can observe two different situations. The first one is very peaked likelihood where the probability of any parameter value far from the MLE is almost close to zero. In the second chart, instead, the curve is flatter and p(MLE) is very close to many sub-optimal states.

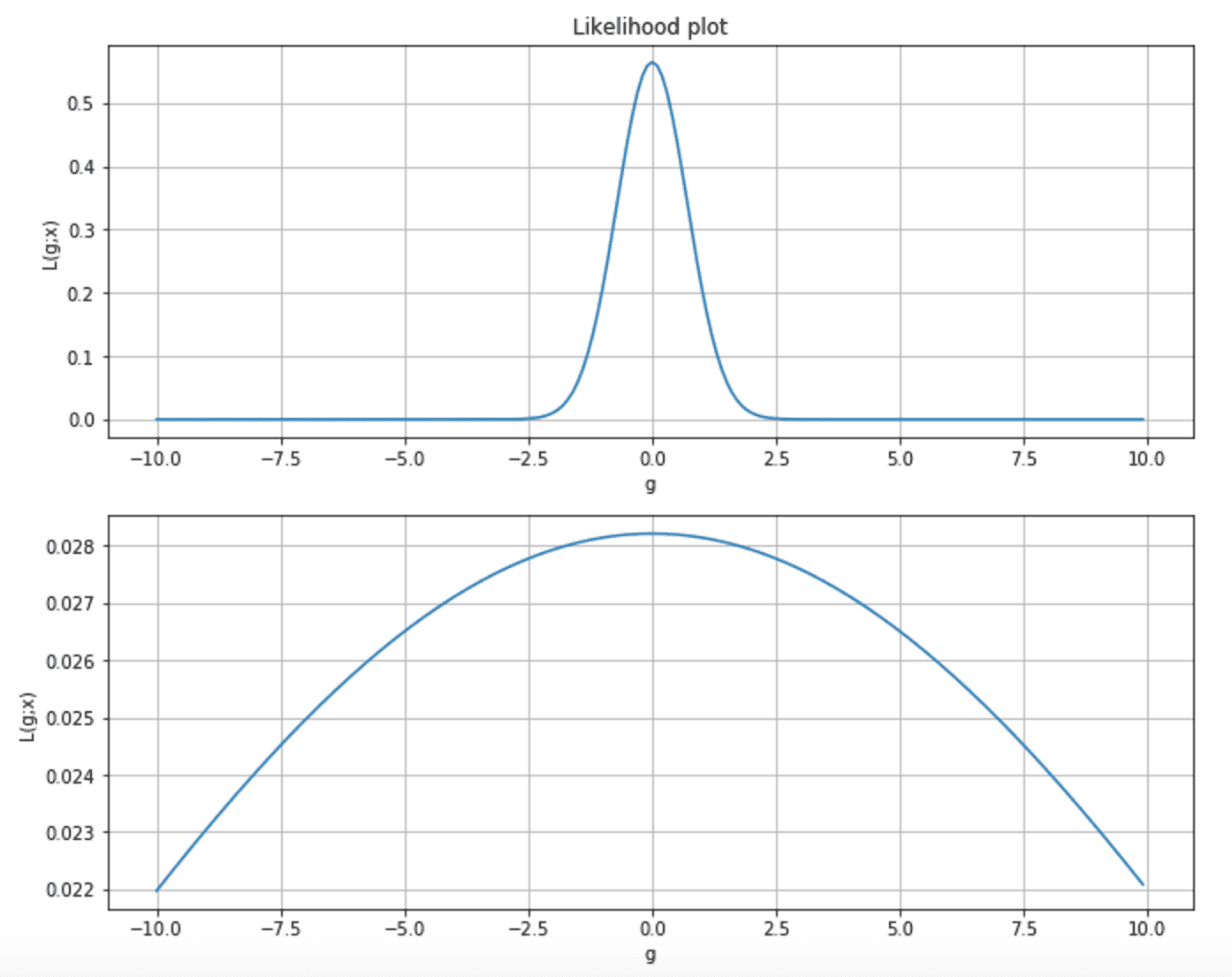
Moreover, as the majority of learning techniques rely on the gradient, in the first case, its magnitude is very when getting close to the MLE, while, in the second, the speed of the gradient is very slow and the learning process can take a quite long time to reach the maximum.

Fisher Information helps in determining how much peaked is the likelihood function and provides a precise measure of the amount of information that the data generating process p(x) can supply to M to reach the MLE. The simplest definition is based on a single parameter ρ. In a discrete form (more common in machine learning), it’s equivalent to:

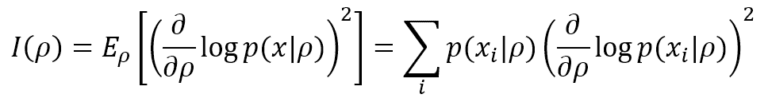
The lower bound is 0, meaning that no information is provided, while there’s no upper bound (+∞). If the model, as often happens, has many parameters (ρ1, ρ2, …, ρN), it’s possible to compute the Fisher Information Matrix, defined as:

Under some regularity conditions, it’s possible to transform both expressions using second derivatives (very often the Fisher Information Matrix) is computed as negative Hessian), however, I prefer to keep the original expressions because they can always be applied without particular restrictions. Even if, without explicit second derivatives, the Fisher Information provides a “speed” of the gradient computed for each parameter. The faster it is, the easier is the learning process.

Now, let’s suppose that we are estimating the value of a parameter ρ, through an approximation ρ′. If E[ρ′] = ρ, the estimator is called unbiased and the only statistical element to into account is the variance. If the expected value is correct, but the variance is very high, the probability of a wrong value is also very high. Therefore, in machine learning, we’re interested in knowing which is the minimum variance of an unbiased estimator. The Cramér-Rao bound states that:

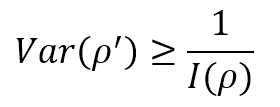
Therefore, a high Fisher Information implies a low variance lower bound, while a low Fisher Information limits our model by imposing a quite high minimum achievable variance. Of course, this doesn’t mean that every unbiased estimator can reach the Cramér-Rao bound, but it provides us with a measure of theoretical maximum accuracy we can achieve if our model is powerful enough.

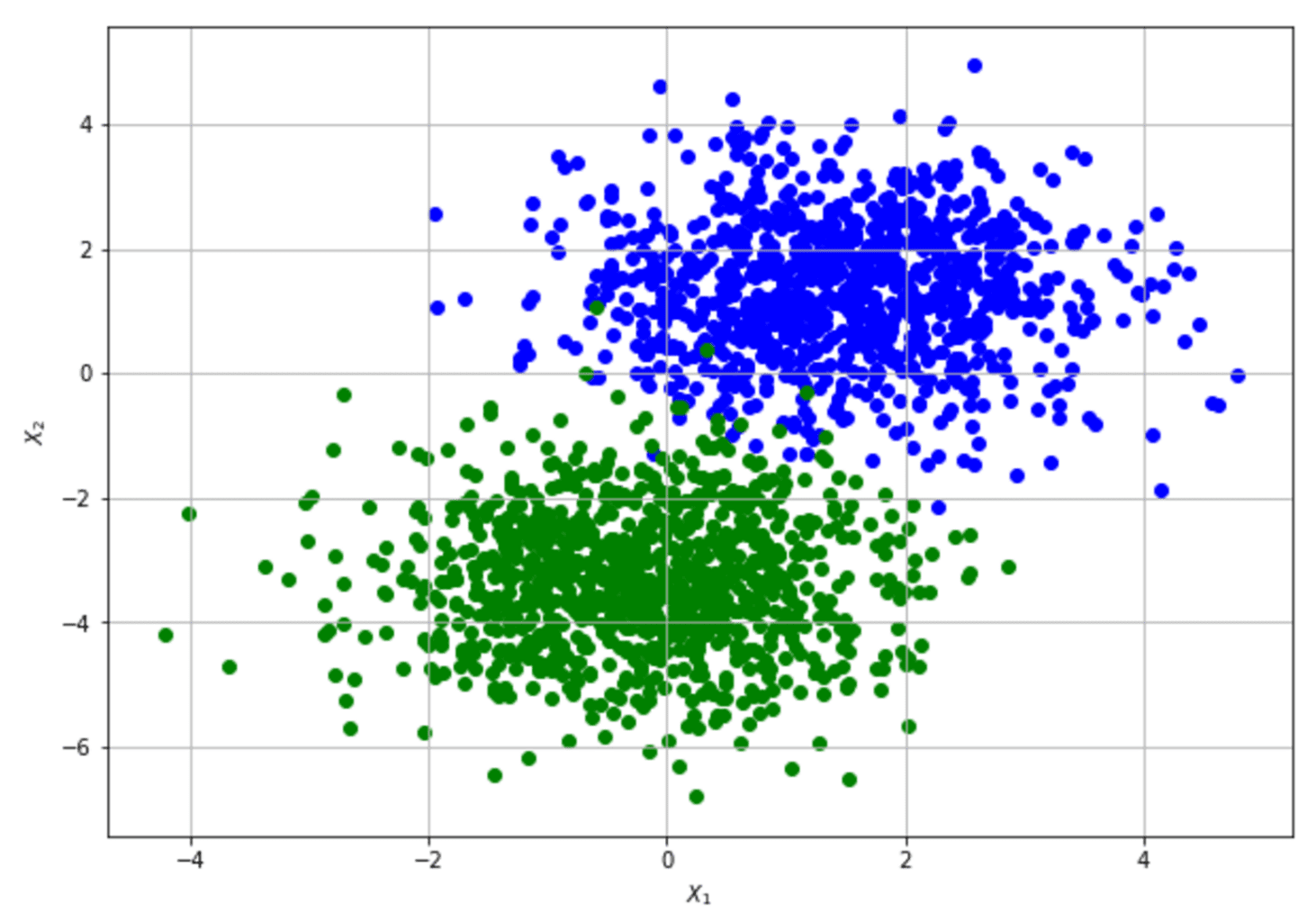
To show how to compute the Fisher Information Matrix and apply the Cramér-Rao bound, let’s consider a very simple dataset (our data generating process) that can be easily learned by a Logistic Regression:

For the sake of simplicity, the 2D data set has been modified adding a “ones” column, so to learn the bias as any other weight. The implementation is based on Tensorflow (available on this GIST), that allows numerically stable gradient computation:

The resulting Fisher Information Matrix is:

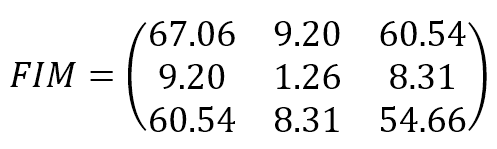
The parameters are (bias, w1, w2). The result shows that the original data set provides a quite high information when estimating the bias and w2 and a lower information for the estimation of w1. The Cramér-Rao bound sets a very small minimum variance for bias and w2 and a relatively higher value for w1. An interpretation of this result can be derived by the structure of the data set: moving along the x2 axis, it’s easy to find a boundary that separates blue and green dots, on the other side, this is not true when exploring the first dimension. On the other side, none of the FIM values are 0 (or very close to 0), meaning that the parameters aren’t orthogonal and they can’t be learned separately.

If you want to obtain an analytic FIM expression, it’s necessary to consider all possible (or a wide set) of values and computing the expected value averaging over ρ.

For a deeper understand about Fisher Information, you see this lecture on Youtube: https://www.youtube.com/watch?v=m1X4uC3hQ_o

See also:

ML Algorithms addendum: Mutual information in classification tasks – Giuseppe Bonaccorso

Many classification algorithms, both in machine and in deep learning, adopt the cross-entropy as cost function. This is a brief explanation why minimizing the cross-entropy allows to increase the mutual information between training and learned distributions.