Let’s consider a Hidden Markov Model describing a sequential problem: a system has three internal (hidden) states:
-
- Ok (Everything works correctly)
- Some issues (not blocking)
- Out of order
However, we can observe only a sensor (globally connected with different sub-systems) whose states are represented by three colors (green, yellow, and red), representing a normal, partially dangerous, and hazardous situation, respectively. They are directly connected with a precise component, so we don’t know if there’s a failure or a false-positive (sometimes another sensor can fail). We can observe this sequence and try to predict the internal states. That’s what you can achieve with HMM. I cannot expose all the theories behind them; however, you can find some good references at the end of this post — this graphical representation of such a process (only five time-steps).

A prediction can be achieved using an algorithm called “Fixed-delay Smoothing,” which combines forward propagation of messages (conditional probabilities of internal states given all sensor data received till a specific time-step) and backward smoothing (past conditional probability tuning). This Python snippet shows how to simulate the process described above:
import numpy as np
from Queue import Queue
class HMM:
def __init__(self, transition_matrix, observation_matrix, delay, initial_state):
self.TM = transition_matrix
self.OM = observation_matrix
self.delay = delay
self.initial_state = np.array(initial_state)
self.events = Queue()
self.t = 0
self.B = np.ndarray(self.TM.shape)
self.forward = np.dot(self.initial_state, self.TM)
self.backward = np.dot(self.initial_state, self.TM)
def predict_state(self, event):
self.events.put_nowait(event)
# Compute diagonal matrix with current event
Ot = self.compute_O_matrix(event)
# Perform fixed-delay smoothing
if self.t > self.delay:
self.forward = self.compute_forward(Ot)
etp = self.events.get_nowait()
Otp = self.compute_O_matrix(etp)
self.B = reduce(np.dot, [np.linalg.inv(Otp), np.linalg.inv(self.TM), self.B, self.TM, Ot])
else:
self.B = reduce(np.dot, [self.B, self.TM, Ot])
self.t += 1
if self.t > self.delay:
return self.normalize(np.dot(self.forward, self.B))
else:
return None
def reset(self):
self.events = Queue()
self.t = 0
self.B = np.ndarray(self.TM.shape)
self.forward = np.dot(self.initial_state, self.TM)
self.backward = np.dot(self.initial_state, self.TM)
def compute_O_matrix(self, event):
return np.diagflat(self.OM[event])
def compute_forward(self, Ot):
return reduce(np.dot, [Ot, self.TM.T, self.forward.T])
def compute_backward(self, Ot):
return reduce(np.dot, [self.TM, Ot, self.backward.T])
@staticmethod
def normalize(x):
return x / np.sum(x)
def log_example(steps=50):
print('Log example')
# Transition probability matrix
# T(i,j) = P(Xt=j | Xt-1=i)
T = np.array([[0.6, 0.3, 0.1],
[0.4, 0.4, 0.2],
[0.1, 0.4, 0.5]])
T_labels = ('Ok', 'Some issues', 'Out of order')
# Observation probability matrix
# O(i,j) = P(event | Xt=i)
O = np.array([[0.8, 0.15, 0.05],
[0.15, 0.7, 0.1],
[0.05, 0.2, 0.75]])
O_labels = ('Green', 'Yellow', 'Red')
hmm = HMM(transition_matrix=T, observation_matrix=O, delay=1, initial_state=[0.5, 0.5, 0.5])
# Prediction
for i in range(1, steps):
observation = np.random.randint(0, len(O_labels))
prediction = hmm.predict_state(observation)
max_value = int(np.argmax(prediction))
if prediction is not None:
print(
'O%d: %s -> %s (%1.3f%%)' % (i, O_labels[observation], T_labels[max_value], prediction[max_value] * 100))
if __name__ == '__main__':
print('HMM simulation')
#rain_example()
log_example()
The result of a simulation example (with all values declared in the snippet) is:
HMM simulation Log example O2: Yellow -> Some issues (76.553%) O3: Red -> Out of order (61.044%) O4: Green -> Ok (70.410%) O5: Red -> Out of order (55.231%) O6: Yellow -> Some issues (78.504%) O7: Yellow -> Some issues (77.122%) O8: Red -> Out of order (60.867%) O9: Yellow -> Some issues (79.078%) O10: Green -> Ok (81.680%) O11: Yellow -> Some issues (69.912%) O12: Green -> Ok (84.343%) O13: Green -> Ok (89.372%) O14: Yellow -> Some issues (69.000%) O15: Green -> Ok (84.513%) O16: Green -> Ok (89.387%) O17: Yellow -> Some issues (68.998%) O18: Green -> Ok (84.514%) O19: Green -> Ok (89.387%) O20: Yellow -> Some issues (68.998%) O21: Green -> Ok (84.514%) O22: Green -> Ok (89.387%) O23: Red -> Out of order (48.530%) O24: Yellow -> Some issues (77.950%) O25: Yellow -> Some issues (76.991%) O26: Red -> Out of order (60.815%) O27: Green -> Ok (70.758%) O28: Green -> Ok (87.973%) O29: Green -> Ok (89.669%) O30: Green -> Ok (89.816%) O31: Green -> Ok (89.829%) O32: Yellow -> Some issues (68.944%) O33: Yellow -> Some issues (75.429%) O34: Yellow -> Some issues (76.240%) O35: Green -> Ok (83.310%) O36: Green -> Ok (89.282%) O37: Red -> Out of order (48.568%) O38: Yellow -> Some issues (77.954%) O39: Green -> Ok (82.139%) O40: Red -> Out of order (50.895%) O41: Red -> Out of order (73.598%) O42: Red -> Out of order (77.923%) O43: Green -> Ok (62.732%) O44: Red -> Out of order (57.583%) O45: Yellow -> Some issues (78.695%) O46: Red -> Out of order (62.948%) O47: Yellow -> Some issues (79.229%) O48: Yellow -> Some issues (77.280%) O49: Red -> Out of order (60.928%)
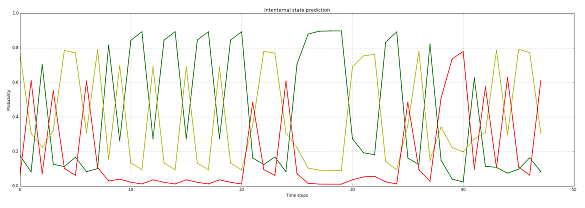
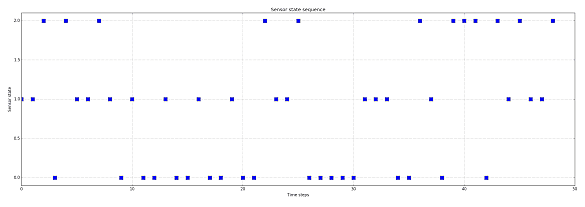
You can notice that a sequence of equal states (confirmed) increases the probability of an internal state, while an abrupt change is not considered immediately with the highest probability. These sequences can also be represented with these plots, which show respectively the sequence of sensor states (low = green, medium = yellow, high = red) and the probabilities of each internal state:
Reference:
-
- Russel S., Norvig P., Artificial Intelligence: a modern approach, Global Edition, Pearson, 2021 (Amazon)
- Wikipedia page about HMM
If you like this post, you can always donate to support my activity! One coffee is enough!