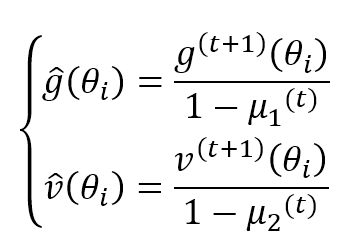Stochastic Gradient Descent (SGD) is a potent technique currently employed to optimize all deep learning models. However, the vanilla algorithm has many limitations, mainly when the system is ill-conditioned and can never find the global minimum. In this post, we will analyze how it works and the most important variations that can speed up the convergence in deep models.
First of all, it’s necessary to standardize the naming. In some books, the expression “Stochastic Gradient Descent” refers to an algorithm operating on a batch size equal to 1. At the same time, “Mini-batch Gradient Descent” is adopted when the batch size exceeds 1. In this context, we assume that Stochastic Gradient Descent operates on batch sizes equal to or greater than 1. In particular, if we define the loss function for a single sample as:
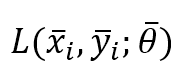
X is the input sample, y is the label(s), and θ is the parameter vector. We can also define the partial cost function considering a batch size equal to N:
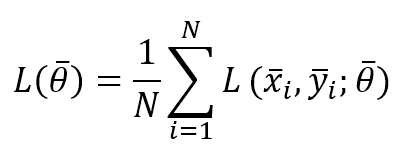
The vanilla Stochastic Gradient Descent algorithm is based on a θ update rule that must move the weights in the opposite directions of the gradient of L (the gradient points always toward a maximum):
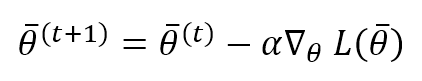
This process is represented in the following figure:
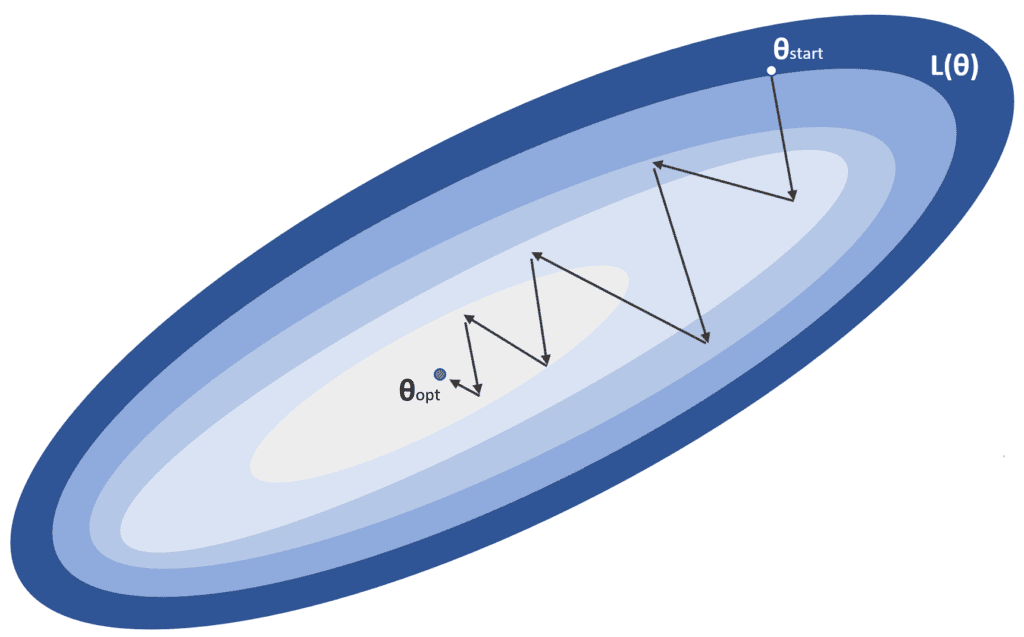
α is the learning rate, while θstart is the initial point, and θopt is the global minimum we’re looking for. In a standard optimization problem, the algorithm converges in a limited number of iterations without particular requirements. Unfortunately, the reality is slightly different, particularly in deep models, where the number of parameters is ten or one hundred million. When the system is relatively shallow, finding local minima where the training process can stop is easier. In contrast, in deeper models, the probability of a local minimum becomes smaller, and saddle points become more and more likely.
To understand this concept, assuming a generic vectorial function L(θ), the conditions for a point to be a minimum are:

Suppose the Hessian matrix is (m x m) where m is the number of parameters. In that case, the second condition is equivalent to say that all m eigenvalues must be non-negative (or that all principal minors composed with the first n rows and n columns must be non-negative).
From a probabilistic viewpoint, P(H positive semi-def.) → 0 when m → ∞, local minima are rare in deep models (this doesn’t mean that local minima are impossible, but their relative weight is lower and lower in deeper models). If the Hessian matrix has both positive and negative eigenvalues (and the gradient is null), the Hessian is said to be indefinite, and the point is called a saddle point. Considering an orthogonal projection, the point is the maximum, and the minimum is for another one. In the following figure, there’s an example created with a 3-dimensional cost function:
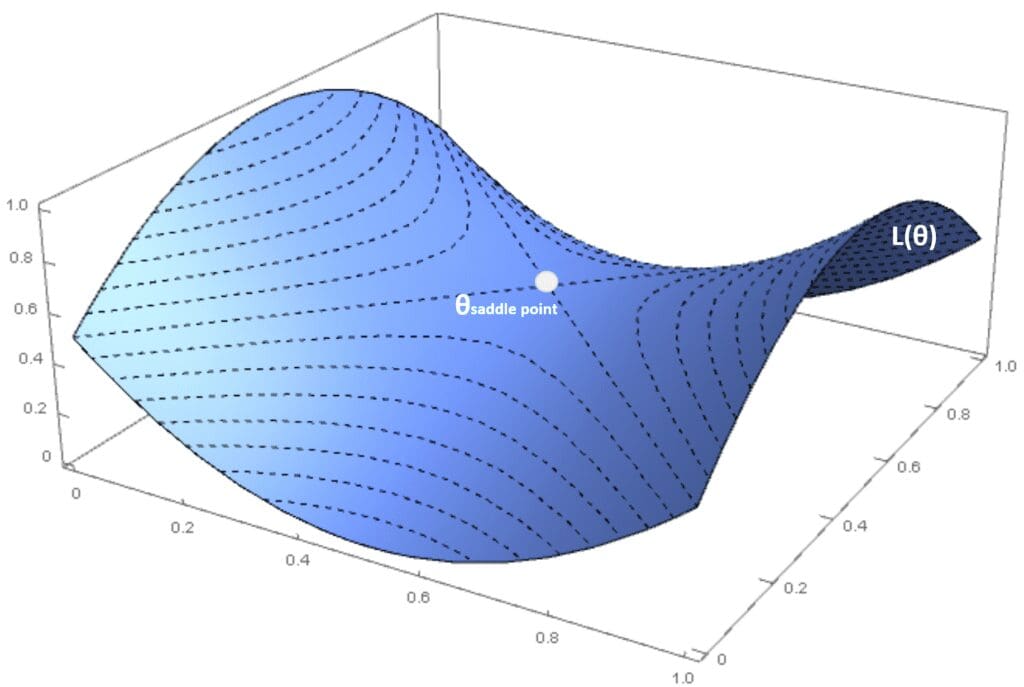
Both local minima and saddle points are problematic, and the optimization algorithm should be able to avoid them. Moreover, there are sometimes conditions called plateaus, where L(θ) is almost flat in a vast region. This drives the gradient to become close to zero, with an increased risk of stopping at a sub-optimal point. This example is shown in the following figure:
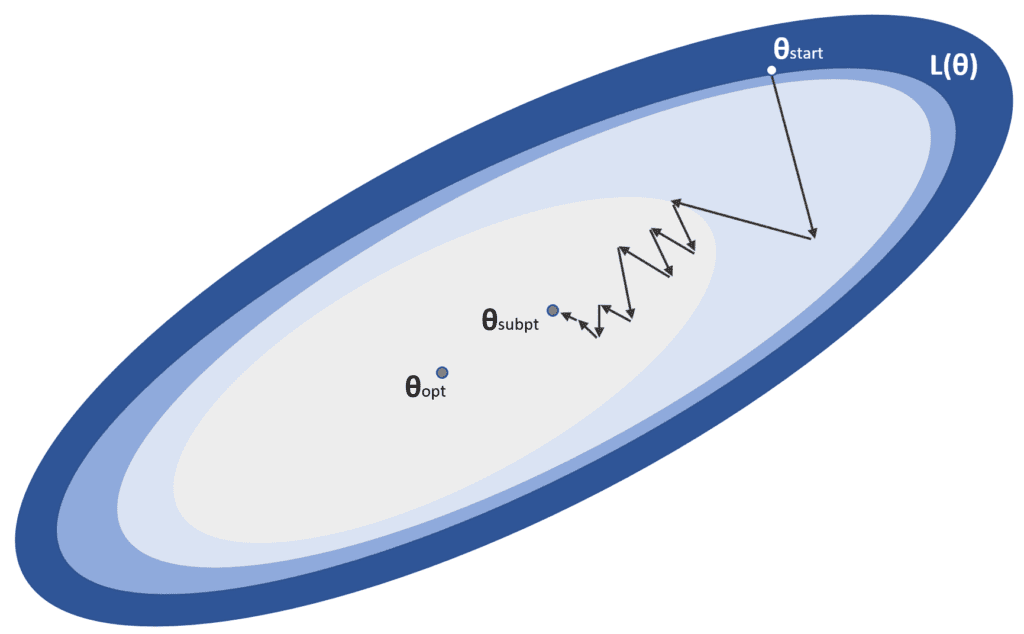
For these reasons, we will discuss some standard methods to improve the performance of a vanilla Stochastic Gradient Descent algorithm.
Gradient Perturbation
A straightforward approach to the problem of plateaus is adding a small noisy term (Gaussian noise) to the gradient:
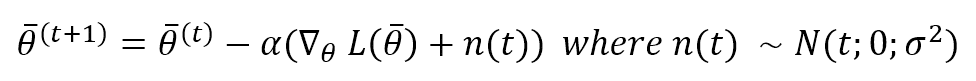
The variance should be carefully chosen (for example, it could decay exponentially during the epochs). However, this method can be a straightforward and effective solution to allow movement even in regions with a zero gradient.
Momentum and Nesterov Momentum
The previous approach was simple, and it can be difficult to implement in many cases. A more robust solution is provided by introducing an exponentially weighted moving average for the gradients. The idea is very intuitive: instead of considering only the current gradient, we can attach part of its history to the correction factor to avoid an abrupt change when the surface becomes flat. The Momentum algorithm is, therefore:
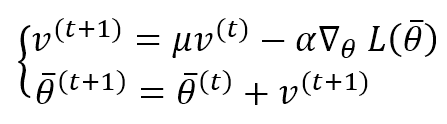
The first equation computes the correction factor considering the weight μ. If μ is small, the previous gradients are soon discarded. If, instead, μ → 1, their effect continues for longer. A typical value in many applications is between 0.75 and 0.99. However, it’s essential to consider μ as a hyperparameter to adjust in every application. The second term performs the parameter update. In the following figure, there’s a vectorial representation of a Momentum step:
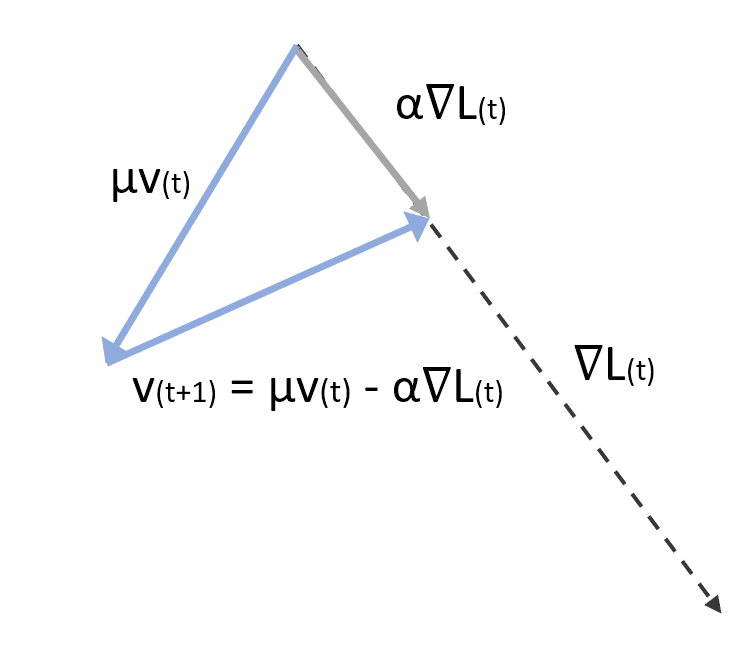
The Nesterov Momentum provides a slightly different variation. The difference with the base algorithm is that we first apply the correction with the current factor v(t) to determine the gradient and then compute v(t+1) and correct the parameters:
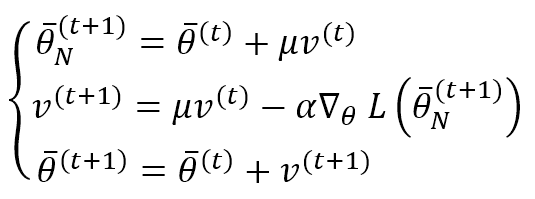
This algorithm can improve the converging speed (Nesterov has theoretically proved the result in the scope of mathematical optimization). However, it doesn’t seem to produce excellent results in deep-learning contexts. It can be implemented alone or with the other algorithms we will discuss.
RMSProp
This algorithm, proposed by G. Hinton, is based on adapting the correction factor for each parameter to increase the effect on slowly changing parameters and reduce it when their change magnitude is huge. This approach can dramatically improve the performance of a deep network, but it’s a little bit more expensive than Momentum because we need to compute a speed term for each parameter:
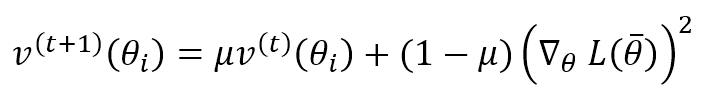
This term computes the exponentially weighted moving average of the gradient squared (element-wise). Like Momentum, μ determines how fast the previous speeds are forgotten. The parameter update rule is:
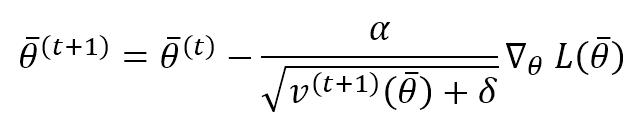
α is the learning rate, and δ is a small constant (~ 1e-6 ÷ 1e-5) introduced to avoid a division by zero when the speed is null. As it’s possible to see, each parameter is updated with a very similar rule to the vanilla Stochastic Gradient Descent. Still, the learning rate is adjusted per single parameter using the reciprocal of the square root of the relative speed. It’s easy to understand that large gradients determine significant speeds and, adaptively, the corresponding update is more minor and vice-versa. RMSProp is a mighty and flexible algorithm, and it is widely used in Deep Reinforcement Learning, CNN, and RNN-based projects.
Adam
Adam is an adaptive algorithm that could be considered an extension of RMSProp. Instead of considering the only exponentially weighted moving average of the gradient square, it also computes the same value for the gradient itself:
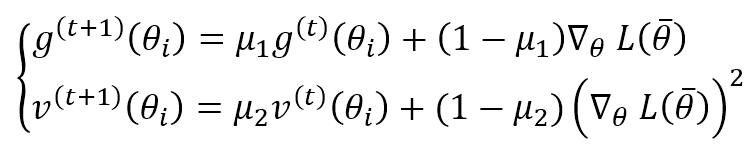
μ1 and μ2 are forgetting factors like in the other algorithms. The authors suggest values greater than 0.9. Both terms are moving estimations of the first and the second moment, so they can be biased (see this article for further information). Adam provided a bias correction for both terms:
The parameter update rule becomes:
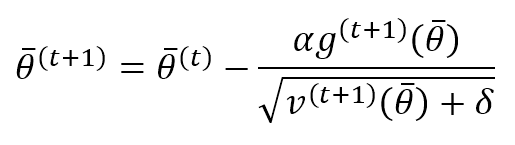
This rule can be considered a standard RMSProp one with a momentum term. The correction term comprises (numerator), the moving average of the gradient, and (denominator), the adaptive factor to modulate the change’s magnitude to avoid changing amplitudes for different parameters. The constant δ, like for RMSProp, should be set equal to 1e-6, and it’s necessary to improve the numerical stability.
AdaGrad
This is another adaptive algorithm based on considering the historical sum of the gradient square and setting the correction factor of a parameter to scale its value with the reciprocal of the squared historical sum. The concept is not very different from RMSProp and Adam, but, in this case, we don’t use an exponentially weighted moving average but the whole history. The accumulation step is:
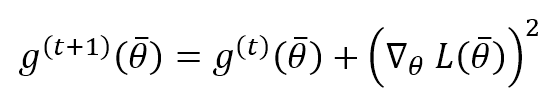
While the update step is exactly as RMSProp:
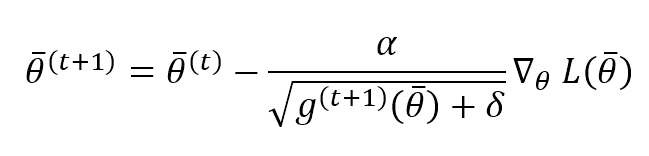
AdaGrad performs well in many tasks, increasing the convergence speed, but it has a drawback deriving from accumulating the whole squared gradient history. As each term is non-negative, g → ∞ and the correction factor (the adaptive learning rate) → 0. Therefore, AdaGrad can produce significant changes during the first iterations, but the change rate is almost null at the end of a long training process.
AdaDelta
AdaDelta is an algorithm proposed by M. D. Zeiler to solve the problem of AdaGrad. The idea is to consider a limited window instead of accumulating the whole history. In particular, this result is achieved using an exponentially weighted moving average (like for RMSProp):
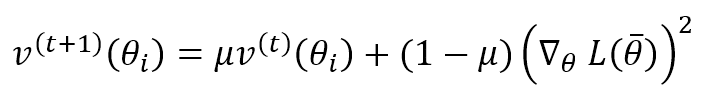
A very interesting expedient introduced by AdaDelta is normalizing the parameter updates to have the same parameter unit. If we consider RMSProp, we have:
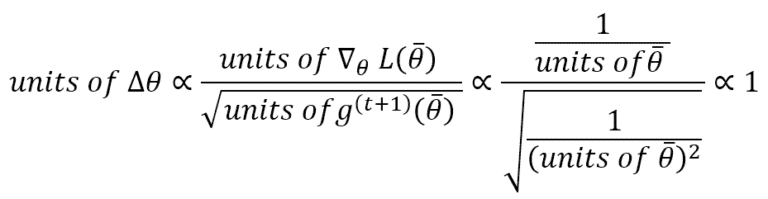
This means that an update is unitless. To avoid this problem, AdaDelta computes the exponentially weighted average of the squared updates and applies this update rule:
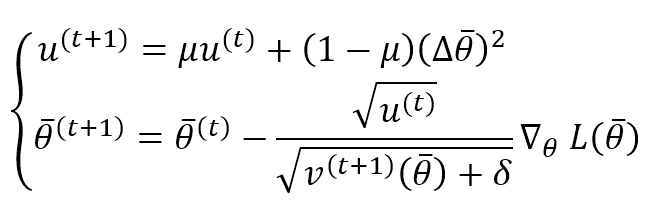
This algorithm performed very well in many deep-learning tasks and is less expensive than AdaGrad. The best value for the constant δ should be assessed through cross-validation. However, 1e-6 is a good default for many tasks, while μ can be set greater than 0.9 to avoid a predominance of old gradients and updates.
Conclusions
Stochastic Gradient Descent is intrinsically a powerful method. However, in non-convex scenarios, its performance can be degraded. We have explored different algorithms (most of them are currently the first choice in deep learning tasks), showing their strengths and weaknesses. Now the question is: which is the best? The answer, unfortunately, doesn’t exist. All of them can perform well in some contexts and poorly in others. All adaptive methods tend to show similar behaviors, but every problem is a separate universe; our only silver bullet is trial and error. I hope the exploration has been clear, and any constructive comments or questions are welcome!
References:
-
- Goodfellow I., Bengio Y., Courville A., Deep Learning, The MIT Press
- Duchi J., Hazan E., Singer Y., Adaptive Subgradient Methods for Online Learning and Stochastic Optimization, Journal of Machine Learning Research 12 (2011) 2121-2159
- Zeiler M. D., AdaDelta: An Adaptive Learning Rate Method, arXiv:1212.5701
If you like this post, you can always donate to support my activity! One coffee is enough!