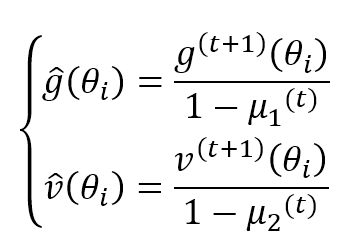La Stochastic Gradient Descent (SGD) è una tecnica molto potente che attualmente viene impiegata per ottimizzare tutti i modelli di apprendimento profondo. Tuttavia, l’algoritmo vanilla ha molte limitazioni, soprattutto quando il sistema è mal condizionato e non può mai trovare il minimo globale. In questo post, analizzeremo come funziona e le variazioni più importanti che possono accelerare la convergenza nei modelli profondi.
Prima di tutto, è necessario standardizzare la denominazione. In alcuni libri, l’espressione “Stochastic Gradient Descent” (discesa del gradiente stocastico) si riferisce a un algoritmo che opera con una dimensione di batch pari a 1. Allo stesso tempo, viene adottato il metodo “Mini-batch Gradient Descent” quando la dimensione del lotto supera 1. In questo contesto, assumiamo che la Discesa Gradiente Stocastica operi su lotti di dimensioni pari o superiori a 1. In particolare, se definiamo la funzione di perdita per un singolo campione come:
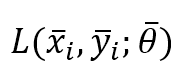
Dove x è il campione di ingresso, y è l’etichetta (o le etichette) e θ è il vettore dei parametri. Possiamo anche definire la funzione di costo parziale considerando una dimensione del lotto pari a N:
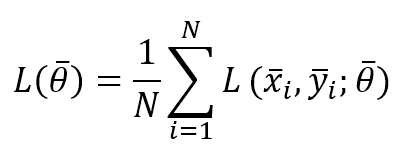
L’algoritmo vanilla Stochastic Gradient Descent si basa su una regola di aggiornamento θ che deve spostare i pesi nelle direzioni opposte del gradiente di L (il gradiente punta sempre verso un massimo):
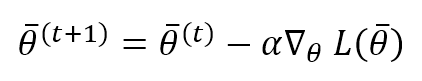
Questo processo è rappresentato nella figura seguente:
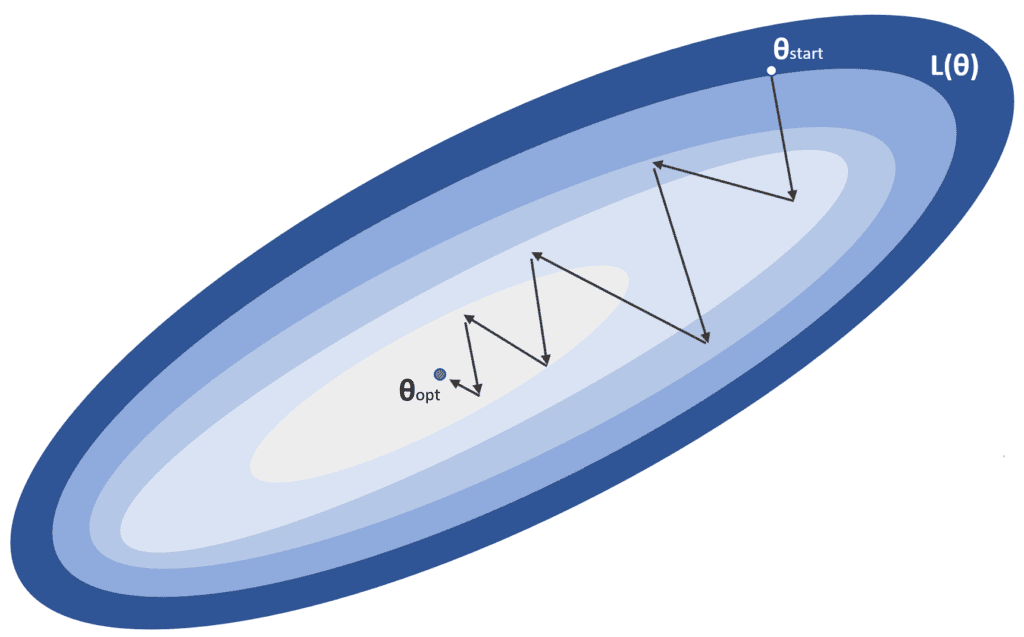
α è il tasso di apprendimento, mentre θstart è il punto iniziale e θopt è il minimo globale che stiamo cercando. In un problema di ottimizzazione standard, l’algoritmo converge in un numero limitato di iterazioni senza particolari requisiti. Purtroppo, la realtà è leggermente diversa, soprattutto nei modelli profondi, dove il numero di parametri è dell’ordine di dieci o cento milioni. Quando il sistema è relativamente poco profondo, è più facile trovare dei minimi locali in cui il processo di addestramento può fermarsi, mentre nei modelli più profondi, la probabilità di un minimo locale si riduce e, invece, i punti di sella diventano sempre più probabili.
Per capire questo concetto, assumendo una funzione vettoriale generica L(θ), le condizioni affinché un punto sia un minimo sono:

Se la matrice Hessiana è (m x m) dove m è il numero di parametri, la seconda condizione è equivalente a dire che tutti gli autovalori m devono essere non negativi (o che tutti i minori principali composti con le prime n righe e n colonne devono essere non negativi).
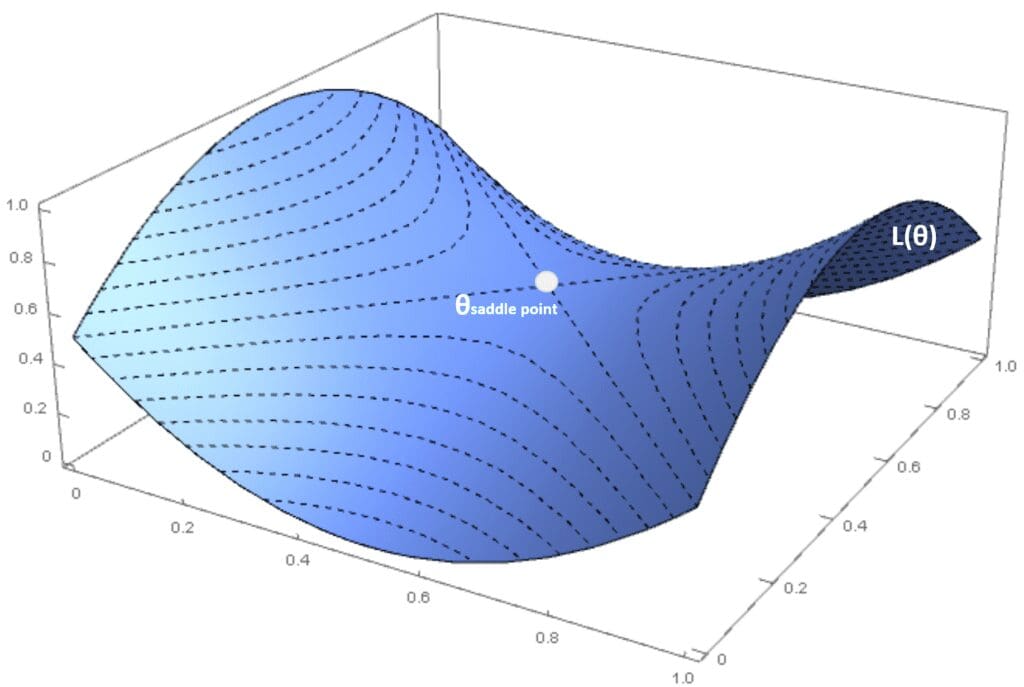
Da un punto di vista probabilistico, P(H positivo semi-def.) → 0 quando m → ∞, i minimi locali sono rari nei modelli profondi (questo non significa che i minimi locali siano impossibili, ma il loro peso relativo è sempre più basso nei modelli profondi). Se la matrice Hessiana ha autovalori sia positivi che negativi (e il gradiente è nullo), si dice che l’Hessiano è indefinito e il punto è chiamato punto di sella. In questo caso, considerando una proiezione ortogonale, il punto è il massimo e il minimo è per un altro. Nella figura seguente, c’è un esempio creato con una funzione di costo tridimensionale:
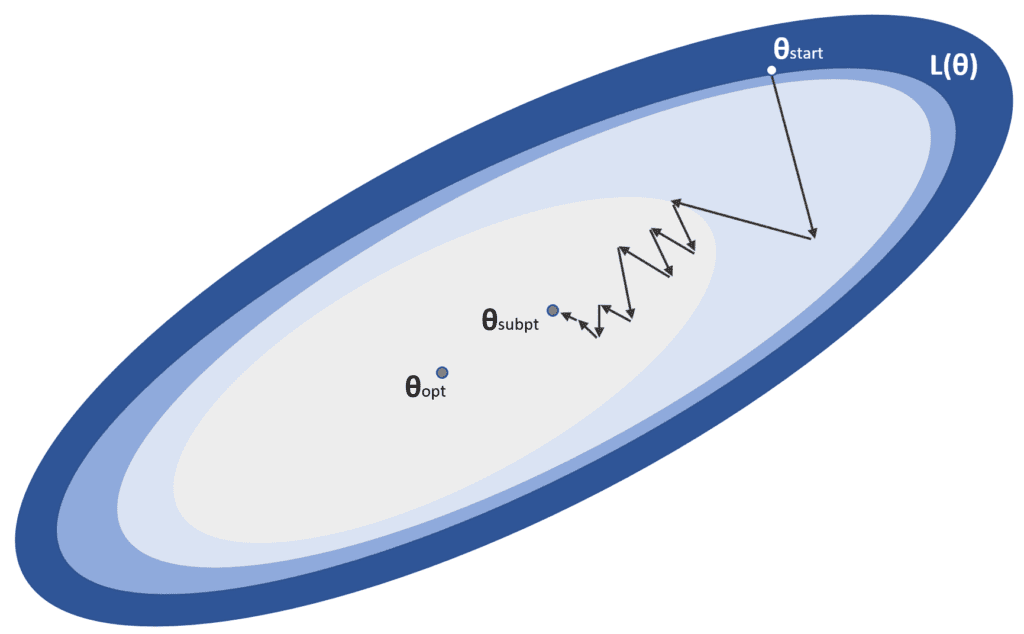
Ovviamente, sia i minimi locali che i punti di sella sono problematici e l’algoritmo di ottimizzazione deve essere in grado di evitarli. Inoltre, a volte esistono delle condizioni chiamate plateau, in cui L(θ) è quasi piatto in una regione molto ampia. Questo porta il gradiente a diventare vicino allo zero, con un rischio maggiore di fermarsi in un punto non ottimale. Questo esempio è mostrato nella figura successiva:
Per questi motivi, ora discuteremo alcuni metodi comuni per migliorare le prestazioni di un algoritmo vanilla Stochastic Gradient Descent.
Perturbazione del gradiente
Un approccio molto semplice al problema dei plateau consiste nell’aggiungere un piccolo termine rumoroso (rumore gaussiano) al gradiente:
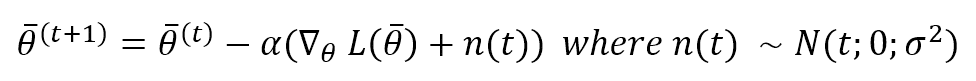
La varianza deve essere scelta con attenzione (ad esempio, potrebbe decadere in modo esponenziale durante le epoche). Tuttavia, questo metodo può essere una soluzione molto semplice ed efficace per consentire il movimento anche nelle regioni con gradiente zero.
Momentum e Momentum Nesterov
L’approccio precedente era piuttosto semplice e può essere difficile da implementare in molti casi. Una soluzione più robusta viene fornita introducendo una media mobile ponderata esponenzialmente per i gradienti. L’idea è molto intuitiva: invece di considerare solo il gradiente attuale, possiamo collegare una parte della sua storia al fattore di correzione, in modo da evitare un cambiamento brusco quando la superficie diventa piatta. L’algoritmoMomentum è, quindi:
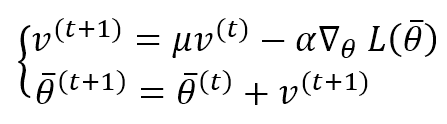
La prima equazione calcola il fattore di correzione considerando il peso μ. Se μ è piccolo, i gradienti precedenti vengono presto scartati. Se, invece, μ → 1, il loro effetto continua più a lungo. Un valore comune in molte applicazioni è compreso tra 0,75 e 0,99. Tuttavia, è importante considerare μ come un iperparametro da regolare in ogni applicazione. Il secondo termine esegue l’aggiornamento dei parametri. Nella figura seguente, c’è una rappresentazione vettoriale di un passo di Momentum:
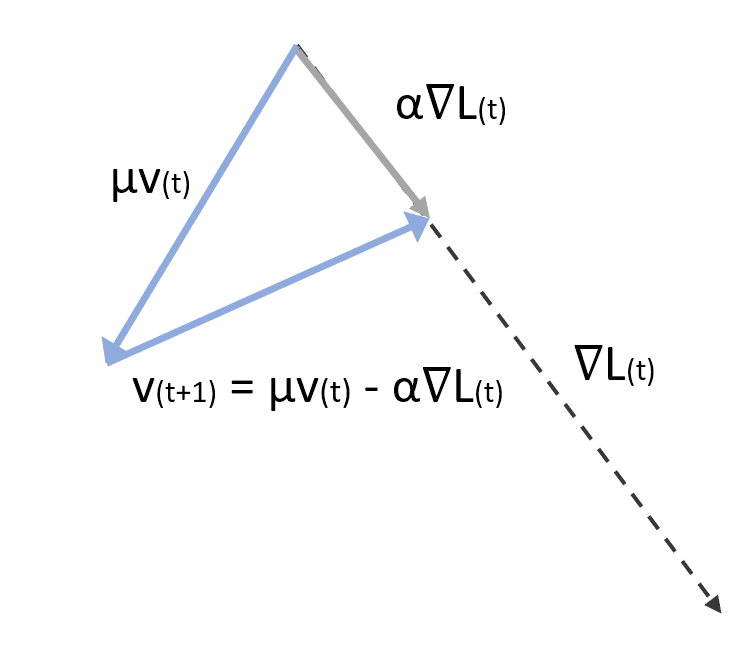
Il Nesterov Momentum offre una variante leggermente diversa. La differenza con l’algoritmo di base è che prima applichiamo la correzione con il fattore corrente v(t) per determinare il gradiente e poi calcoliamo v(t+1) e correggiamo i parametri:
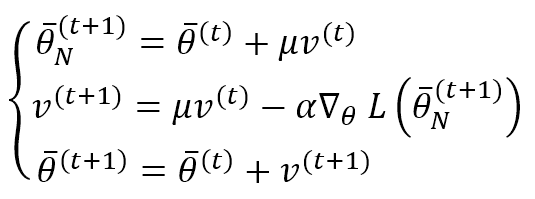
Questo algoritmo può migliorare la velocità di convergenza (il risultato è stato dimostrato teoricamente da Nesterov nell’ambito dell’ottimizzazione matematica). Tuttavia, non sembra produrre risultati eccellenti nei contesti di apprendimento profondo. Può essere implementato da solo o in combinazione con gli altri algoritmi di cui parleremo.
RMSProp
Questo algoritmo, proposto da G. Hinton, si basa sull’idea di adattare il fattore di correzione per ogni parametro per aumentare l’effetto sui parametri che cambiano lentamente e ridurlo quando la loro entità di cambiamento è molto grande. Questo approccio può migliorare notevolmente le prestazioni di una rete profonda, ma è un po’ più costoso di Momentum, perché dobbiamo calcolare un termine di velocità per ogni parametro:
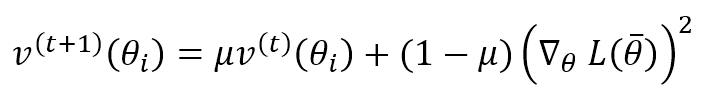
Questo termine calcola la media mobile ponderata esponenzialmente del gradiente al quadrato (in base agli elementi). Come il Momento, μ determina la velocità con cui vengono dimenticate le velocità precedenti. La regola di aggiornamento dei parametri è:
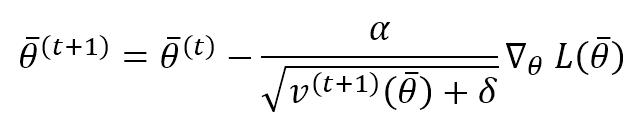
α è il tasso di apprendimento e δ è una piccola costante (~ 1e-6 ÷ 1e-5) introdotta per evitare una divisione per zero quando la velocità è nulla. Come si può vedere, ogni parametro viene aggiornato con una regola molto simile a quella del metodo vanilla Stochastic Gradient Descent. Tuttavia, il tasso di apprendimento effettivo viene regolato per singolo parametro utilizzando il reciproco della radice quadrata della velocità relativa. È facile capire che grandi gradienti determinano grandi velocità e, in modo adattivo, l’aggiornamento corrispondente è più piccolo e viceversa. RMSProp è un algoritmo molto potente e flessibile, ed è ampiamente utilizzato nei progetti basati su Deep Reinforcement Learning, CNN e RNN.
Adam
Adam è un algoritmo adattivo che potrebbe essere considerato un’estensione di RMSProp. Invece di considerare l’unica media mobile ponderata esponenzialmente del quadrato del gradiente, calcola anche lo stesso valore per il gradiente stesso:
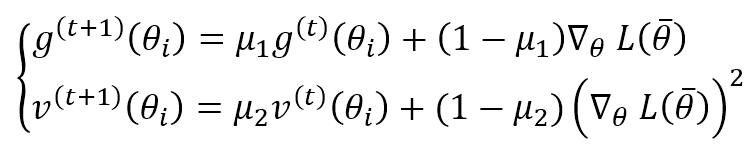
μ1 e μ2 sono fattori di dimenticanza come negli altri algoritmi. Gli autori suggeriscono valori superiori a 0,9. Entrambi i termini sono stime in movimento del primo e del secondo momento, quindi possono essere distorti (per ulteriori informazioni, consulti questo articolo ). Adam ha fornito una correzione del pregiudizio per entrambi i termini:
La regola di aggiornamento dei parametri diventa:
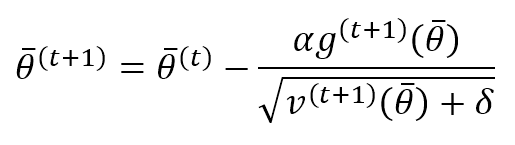
Questa regola può essere considerata come una regola RMSProp standard con un termine di slancio. Infatti, il termine di correzione comprende (numeratore), la media mobile del gradiente, e (denominatore), il fattore adattivo per modulare l’entità della variazione per evitare ampiezze di cambiamento diverse per parametri diversi. La costante δ, come per RMSProp, deve essere impostata pari a 1e-6, ed è necessaria per migliorare la stabilità numerica.
AdaGrad
Si tratta di un altro algoritmo adattivo basato sulla considerazione della somma storica del quadrato del gradiente e sull’impostazione del fattore di correzione di un parametro per scalare il suo valore con il reciproco della somma storica al quadrato. Il concetto non è molto diverso da quello di RMSProp e Adam, ma, in questo caso, non utilizziamo una media mobile ponderata esponenzialmente, ma l’intera storia. La fase di accumulo è:
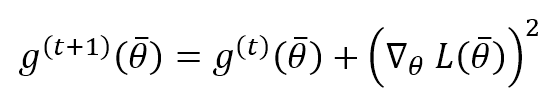
Mentre la fase di aggiornamento è esattamente come RMSProp:
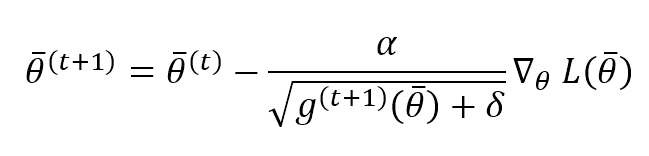
AdaGrad si comporta bene in molti compiti, aumentando la velocità di convergenza, ma presenta uno svantaggio derivante dall’accumulo dell’intera storia del gradiente quadratico. Dato che ogni termine è non negativo, g → ∞ e il fattore di correzione (che è il tasso di apprendimento adattivo) → 0. Pertanto, durante le prime iterazioni, AdaGrad può produrre cambiamenti significativi, ma il tasso di cambiamento è quasi nullo alla fine di un lungo processo di formazione.
AdaDelta
AdaDelta è un algoritmo proposto da M. D. Zeiler per risolvere il problema di AdaGrad. L’idea è di considerare una finestra limitata invece di accumulare l’intera storia. In particolare, questo risultato si ottiene utilizzando una media mobile ponderata esponenzialmente (come per RMSProp):
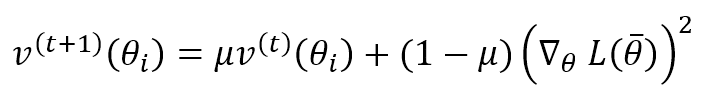
Un espediente molto interessante introdotto da AdaDelta è la normalizzazione degli aggiornamenti dei parametri, in modo da avere la stessa unità del parametro. Infatti, se consideriamo RMSProp, abbiamo:
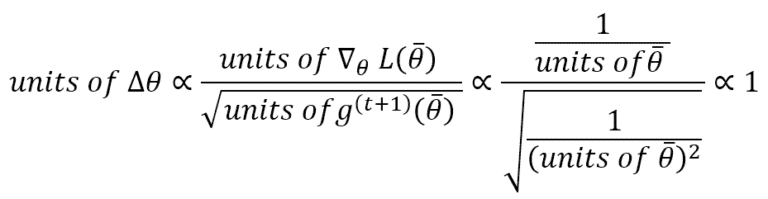
Ciò significa che un aggiornamento è privo di unità. Per evitare questo problema, AdaDelta calcola la media ponderata esponenziale degli aggiornamenti al quadrato e applica questa regola di aggiornamento:
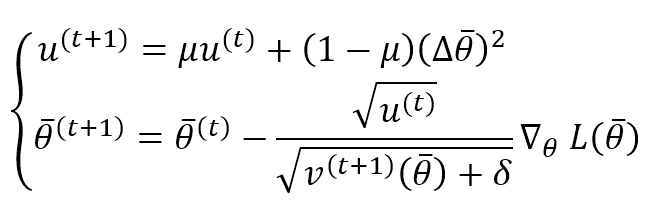
Questo algoritmo si è comportato molto bene in molti compiti di apprendimento profondo ed è meno costoso di AdaGrad. Il valore migliore per la costante δ deve essere valutato attraverso una convalida incrociata. Tuttavia, 1e-6 è un buon valore predefinito per molti compiti, mentre μ può essere impostato maggiore di 0,9 per evitare una predominanza di gradienti e aggiornamenti vecchi.
Conclusioni
La discesa stocastica del gradiente è intrinsecamente un metodo potente, tuttavia, in scenari non convessi, le sue prestazioni possono essere degradate. Abbiamo esplorato diversi algoritmi (la maggior parte di essi sono attualmente la prima scelta nei compiti di apprendimento profondo), mostrando i loro punti di forza e di debolezza. Ora la domanda è: qual è il migliore? La risposta, purtroppo, non esiste. Tutti possono avere un buon rendimento in alcuni contesti e un cattivo rendimento in altri. In generale, tutti i metodi adattivi tendono a mostrare comportamenti simili, ma ogni problema è un universo a sé stante; la nostra unica strategia vincente è la prova e l’errore. Spero che l’esplorazione sia stata chiara, e ogni commento o domanda costruttiva è benvenuta!
Riferimenti:
-
- Goodfellow I., Bengio Y., Courville A., Deep Learning, The MIT Press
- Duchi J., Hazan E., Singer Y., Adaptive Subgradient Methods for Online Learning and Stochastic Optimization, Journal of Machine Learning Research 12 (2011) 2121-2159
- Zeiler M. D., AdaDelta: An Adaptive Learning Method, arXiv:1212.5701
Se ti piace l’articolo, puoi sempre fare una donazione per supportare la mia attività. Basta un caffè!