Gli algoritmi passivi aggressivi sono una famiglia di algoritmi di apprendimento online (sia per la classificazione che per la regressione) proposti da Crammer et al. L’idea è semplice e le loro prestazioni si sono dimostrate superiori a quelle di altri metodi alternativi come Perceptron Online e MIRA (vedere il documento originale nella sezione di riferimento).
Classificazione
Supponiamo di avere un set di dati:
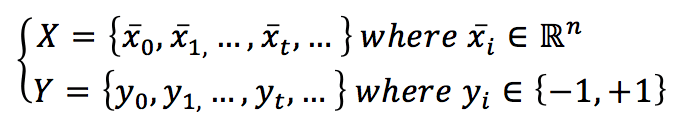
L’indice t è stato scelto per contrassegnare la dimensione temporale. In questo caso, infatti, i campioni possono continuare ad arrivare per un tempo indefinito. Naturalmente, supponiamo che vengano estratti dalla stessa distribuzione di dati. In questo caso, l’algoritmo continuerà ad apprendere (probabilmente senza grandi modifiche dei parametri). Tuttavia, se vengono estratti da una distribuzione completamente diversa, i pesi dimenticheranno lentamente quella precedente e impareranno la nuova distribuzione. Per semplicità, assumiamo anche che stiamo lavorando con una classificazione binaria basata su etichette bipolari.
Dato un vettore di pesi w, la predizione si ottiene come:
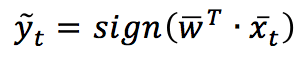
Tutti questi algoritmi si basano sulla funzione di perdita Hinge (la stessa utilizzata da SVM):
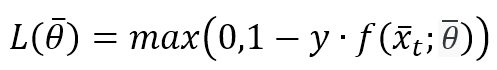
Il valore di L è limitato tra 0 (che significa corrispondenza perfetta) e K che dipende da f(x(t),θ) con K>0 (previsione completamente errata). Un algoritmo passivo-aggressivo funziona genericamente con questa regola di aggiornamento:
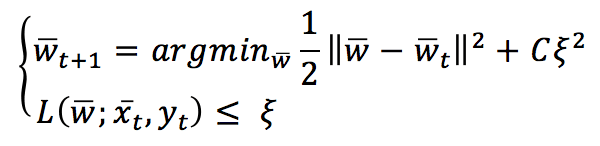
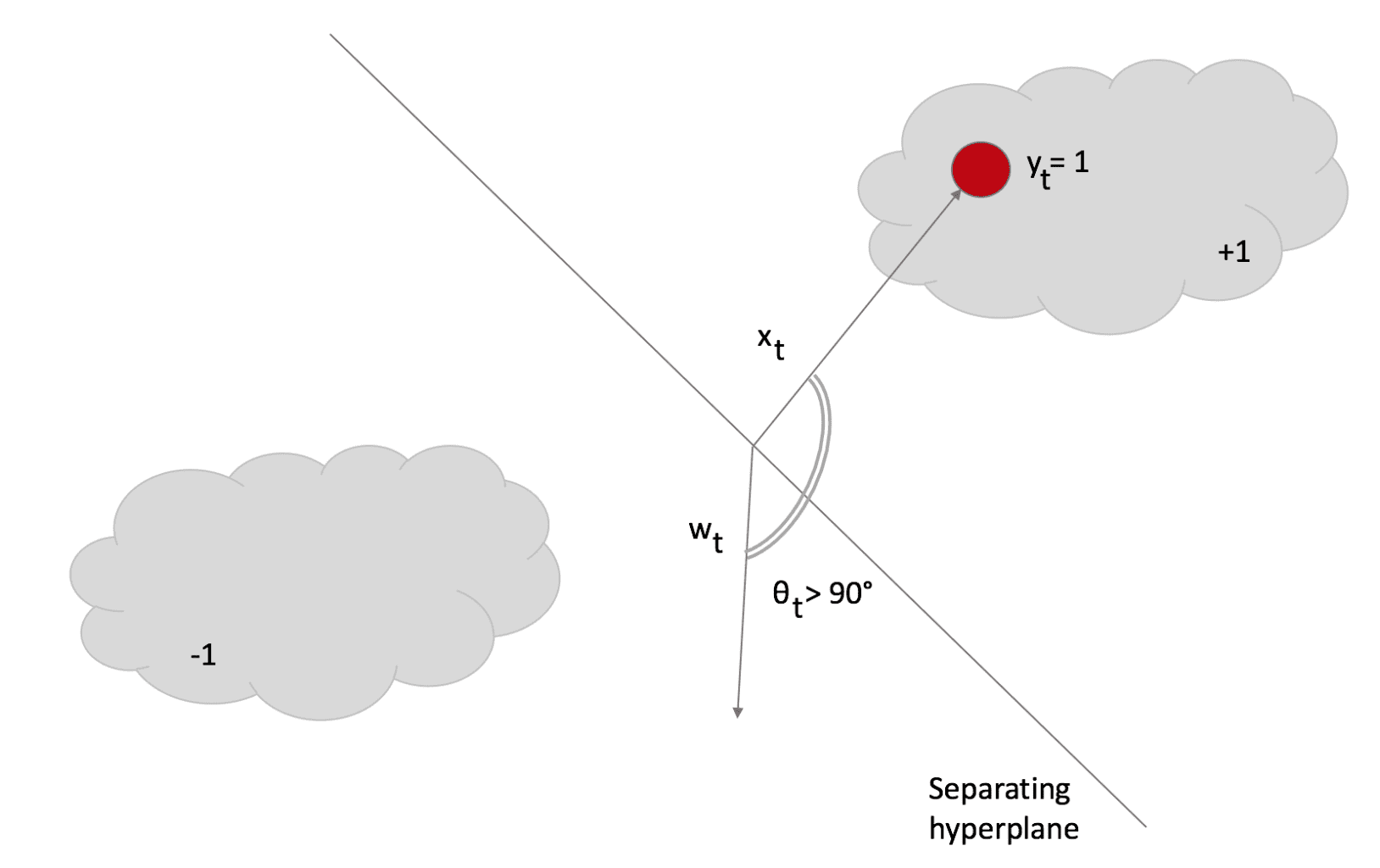
Per capire questa regola, ipotizziamo che la variabile slack ξ=0 (e L vincolata a 0). Se viene presentato un campione x(t), il classificatore utilizza il vettore di pesi corrente per determinare il segno. Se il segno è corretto, la funzione di perdita è 0 e l’argmin è w(t). Ciò significa che l’algoritmo è passivo quando si verifica una classificazione corretta. Supponiamo ora che si sia verificato un errore di classificazione:
L’angolo θ > 90°; pertanto, il prodotto del punto è negativo e il campione viene classificato come -1. Tuttavia, la sua etichetta è +1. In questo caso, la regola di aggiornamento diventa molto aggressiva perché cerca un nuovo w, che deve essere il più vicino possibile al precedente (altrimenti, la conoscenza esistente viene immediatamente persa). Tuttavia, deve soddisfare L=0 (in altre parole, la classificazione deve essere corretta).
L’introduzione della variabile slack consente margini morbidi (come in SVM) e un grado di tolleranza controllato dal parametro C. In particolare, la funzione di perdita deve essere L <= ξ, consentendo un errore maggiore. Valori C più alti producono una maggiore aggressività (con un conseguente rischio più elevato di destabilizzazione in presenza di rumore), mentre valori più bassi consentono un migliore adattamento. Infatti, quando si lavora online, questo tipo di algoritmo deve far fronte a campioni rumorosi (con etichette sbagliate). È necessaria una buona robustezza; altrimenti, cambiamenti troppo rapidi produrranno di conseguenza tassi di errore di classificazione più elevati.
Dopo aver risolto entrambe le condizioni di aggiornamento, otteniamo la regola di aggiornamento in forma chiusa:
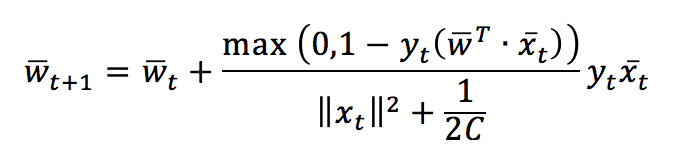
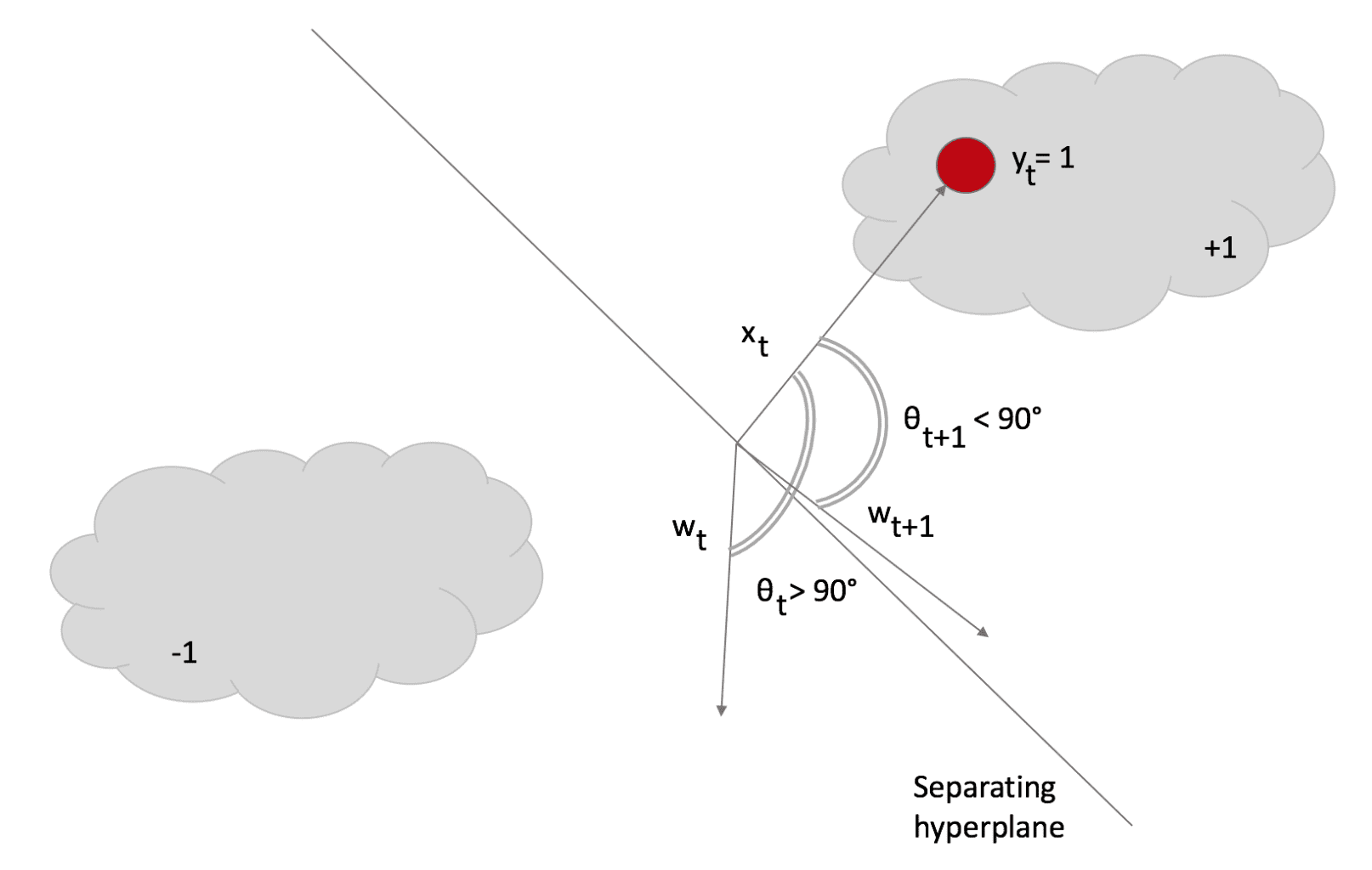
Questa regola conferma le nostre aspettative: il vettore peso viene aggiornato con un fattore il cui segno è determinato da y(t) e la cui grandezza è proporzionale all’errore. Si noti che se non c’è un errore di classificazione, il nominatore diventa 0, quindi w(t+1) = w(t), mentre, in caso di errore di classificazione, w ruoterà verso x(t) e si fermerà con una perdita L <= ξ. Nella figura successiva, l’effetto è stato contrassegnato per mostrare la rotazione. Tuttavia, normalmente è il più piccolo possibile:
Dopo la rotazione, θ < 90° e il prodotto del punto diventa negativo, quindi il campione viene classificato correttamente come +1. Scikit-Learn implementa algoritmi passivi-aggressivi, ma ho preferito implementare il codice per mostrare quanto siano semplici. Nel prossimo frammento (disponibile anche in questo GIST), creo prima un set di dati, poi calcolo il punteggio con una Regressione Logistica, infine applico la PA e misuro il punteggio finale su un set di test:
import numpy as np
from sklearn.datasets import make_classification
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
# Set random seed (for reproducibility)
np.random.seed(1000)
nb_samples = 5000
nb_features = 4
# Create the dataset
X, Y = make_classification(n_samples=nb_samples,
n_features=nb_features,
n_informative=nb_features - 2,
n_redundant=0,
n_repeated=0,
n_classes=2,
n_clusters_per_class=2)
# Split the dataset
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.35, random_state=1000)
# Perform a logistic regression
lr = LogisticRegression()
lr.fit(X_train, Y_train)
print('Logistic Regression score: {}'.format(lr.score(X_test, Y_test)))
# Set the y=0 labels to -1
Y_train[Y_train==0] = -1
Y_test[Y_test==0] = -1
C = 0.01
w = np.zeros((nb_features, 1))
# Implement a Passive Aggressive Classification
for i in range(X_train.shape[0]):
xi = X_train[i].reshape((nb_features, 1))
loss = max(0, 1 - (Y_train[i] * np.dot(w.T, xi)))
tau = loss / (np.power(np.linalg.norm(xi, ord=2), 2) + (1 / (2*C)))
coeff = tau * Y_train[i]
w += coeff * xi
# Compute accuracy
Y_pred = np.sign(np.dot(w.T, X_test.T))
c = np.count_nonzero(Y_pred - Y_test)
print('PA accuracy: {}'.format(1 - float(c) / X_test.shape[0]))
Regressione
Per la regressione, l’algoritmo è molto simile, ma ora si basa su una funzione di perdita Hinge leggermente diversa (chiamata ε-insensibile):
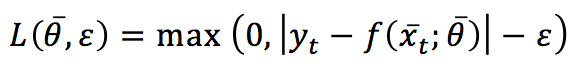
Il parametro ε determina una tolleranza per gli errori di previsione. Le condizioni di aggiornamento sono le stesse adottate per i problemi di classificazione e la regola di aggiornamento risultante è:
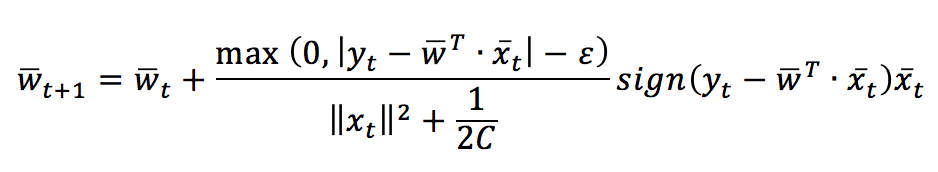
Come per la classificazione, Scikit-Learn implementa anche una regressione. Tuttavia, nello snippet successivo (disponibile anche in questo GIST), c’è un’implementazione personalizzata:
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_regression
# Set random seed (for reproducibility)
np.random.seed(1000)
nb_samples = 500
nb_features = 4
# Create the dataset
X, Y = make_regression(n_samples=nb_samples,
n_features=nb_features)
# Implement a Passive Aggressive Regression
C = 0.01
eps = 0.1
w = np.zeros((X.shape[1], 1))
errors = []
for i in range(X.shape[0]):
xi = X[i].reshape((X.shape[1], 1))
yi = np.dot(w.T, xi)
loss = max(0, np.abs(yi - Y[i]) - eps)
tau = loss / (np.power(np.linalg.norm(xi, ord=2), 2) + (1 / (2*C)))
coeff = tau * np.sign(Y[i] - yi)
errors.append(np.abs(Y[i] - yi)[0, 0])
w += coeff * xi
# Show the error plot
fig, ax = plt.subplots(figsize=(16, 8))
ax.plot(errors)
ax.set_xlabel('Time')
ax.set_ylabel('Error')
ax.set_title('Passive Aggressive Regression Absolute Error')
ax.grid()
plt.show()
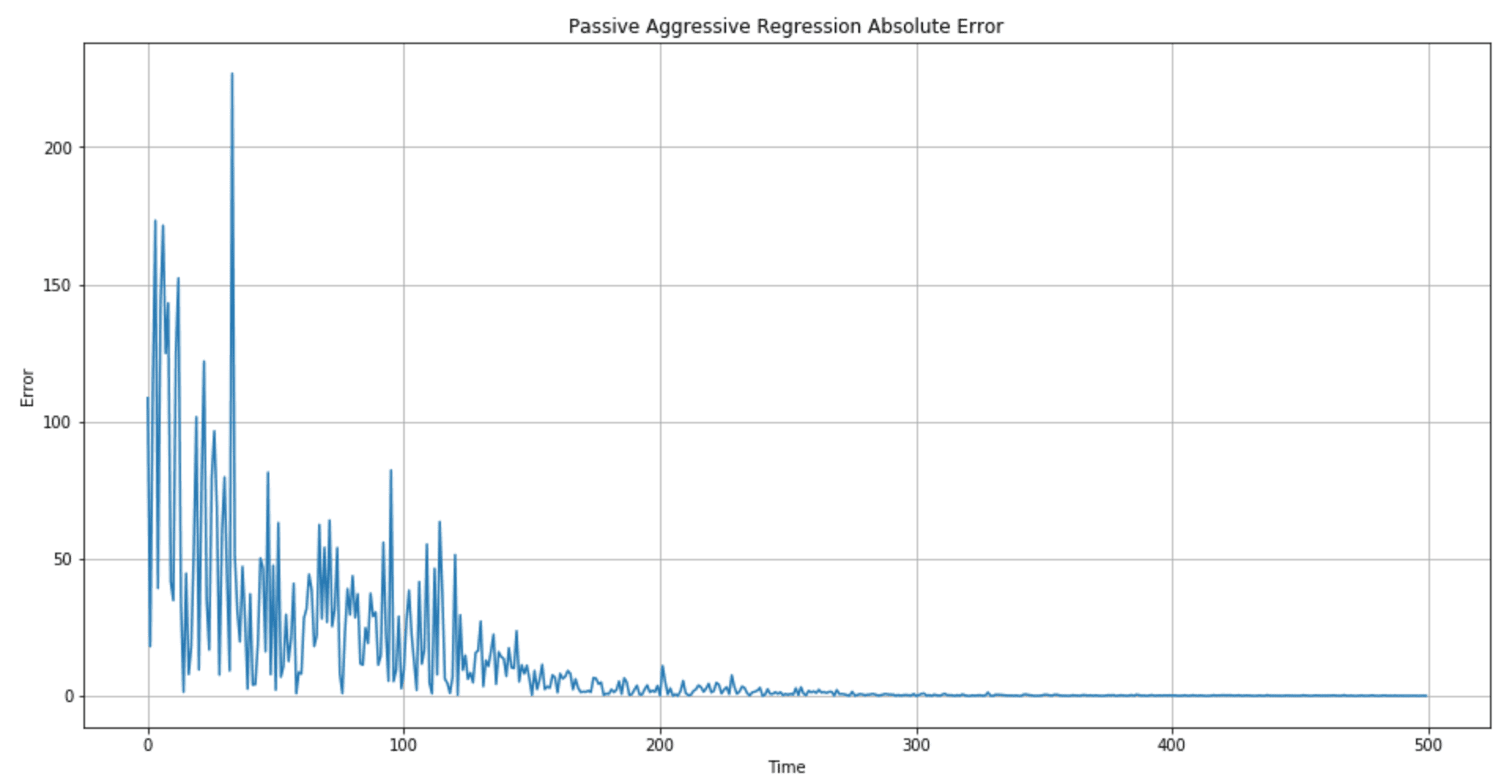
Il grafico degli errori è mostrato nella figura seguente:
La qualità della regressione (in particolare, la durata del periodo transitorio in cui l’errore è elevato) può essere controllata scegliendo valori migliori di C ed ε. In particolare, suggerisco di verificare diversi centri di gamma per C (100, 10, 1, 0,1, 0,01) per determinare se è preferibile un’aggressività maggiore.
Riferimenti:
-
- Crammer K., Dekel O., Keshet J., Shalev-Shwartz S., Singer Y., Online Passive-Aggressive Algorithms, Journal of Machine Learning Research 7 (2006) 551-585
Se ti piace l’articolo, puoi sempre fare una donazione per supportare la mia attività. Basta un caffè!