Molti algoritmi di classificazione nell’apprendimento automatico e profondo adottano l’entropia congiunta come funzione di costo. Questo spiega brevemente perché la minimizzazione dell’entropia congiunta aumenta l’informazione mutua tra le distribuzioni di formazione e di apprendimento.
Se chiamiamo p la distribuzione di probabilità dell’insieme di formazione e q quella corrispondente appresa, l’entropia congiunta è:
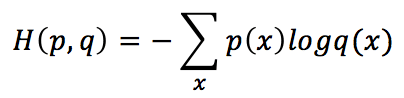
Manipolando questa espressione, otteniamo:
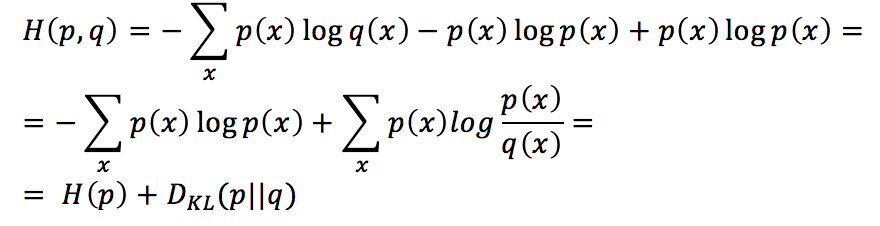
Pertanto, l’entropia incrociata è uguale alla somma di H(p), che è l’entropia della distribuzione di formazione (che non possiamo controllare), e la divergenza di Kullback-Leibler della distribuzione appresa da quella di formazione. Poiché il primo termine è una costante, la minimizzazione dell’entropia congiunta è equivalente alla minimizzazione della divergenza di Kullback-Leibler.
Noi sappiamo che:
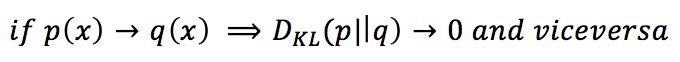
Pertanto, il processo di formazione ‘rimodellerà’ q(x) per minimizzare la sua divergenza da p(x). Nella figura seguente, c’è una rappresentazione schematica di questo processo prima dell’iterazione iniziale, all’iterazione n e alla fine del processo di formazione:
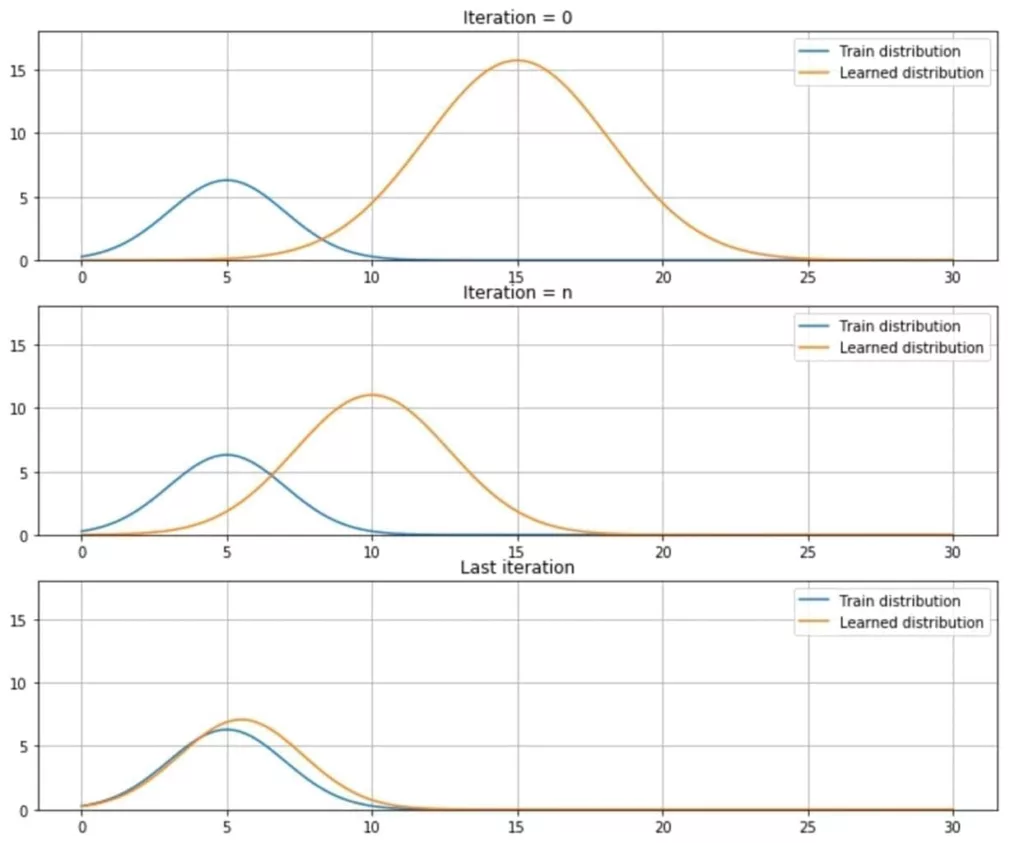
Se consideriamo l’informazione mutua tra p(x) e q(x), otteniamo:
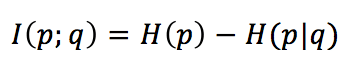
L’informazione reciproca è la quantità di informazioni condivise da entrambe le distribuzioni. Si esprime come l’entropia della distribuzione di addestramento meno l’incertezza ‘non risolta’ che q fornisce quando viene scelta al posto di p. In altre parole, se abbiamo modellato perfettamente q, significa che q = p; quindi, H(q|q) = 0 e I(p;q) = H(p) (che rappresenta la quantità massima di informazione che possiamo apprendere). Pertanto, quando minimizziamo l’entropia congiunta, minimizziamo implicitamente l’entropia condizionale H(p|q), massimizzando l’informazione mutua.
Un buon libro introduttivo sulla Teoria dell’Informazione:
Se ti piace l’articolo, puoi sempre fare una donazione per supportare la mia attività. Basta un caffè!


