Many classification algorithms in machine and deep learning adopt cross-entropy as a cost function. This briefly explains why minimizing the cross-entropy increases the mutual information between training and learning distributions.
If we call p the training set probability distribution and q, the corresponding learned one, the cross-entropy is:
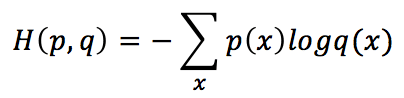
By manipulating this expression, we get:
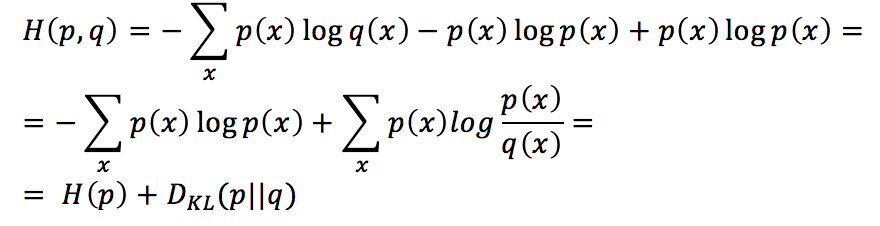
Therefore, the cross-entropy is equal to the sum of H(p), which is the entropy of the training distribution (that we can’t control), and the Kullback-Leibler divergence of the learned distribution from the training one. As the first term is a constant, minimizing the cross-entropy is equivalent to minimizing the Kullback-Leibler divergence.
We know that:
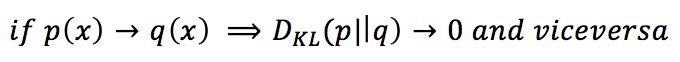
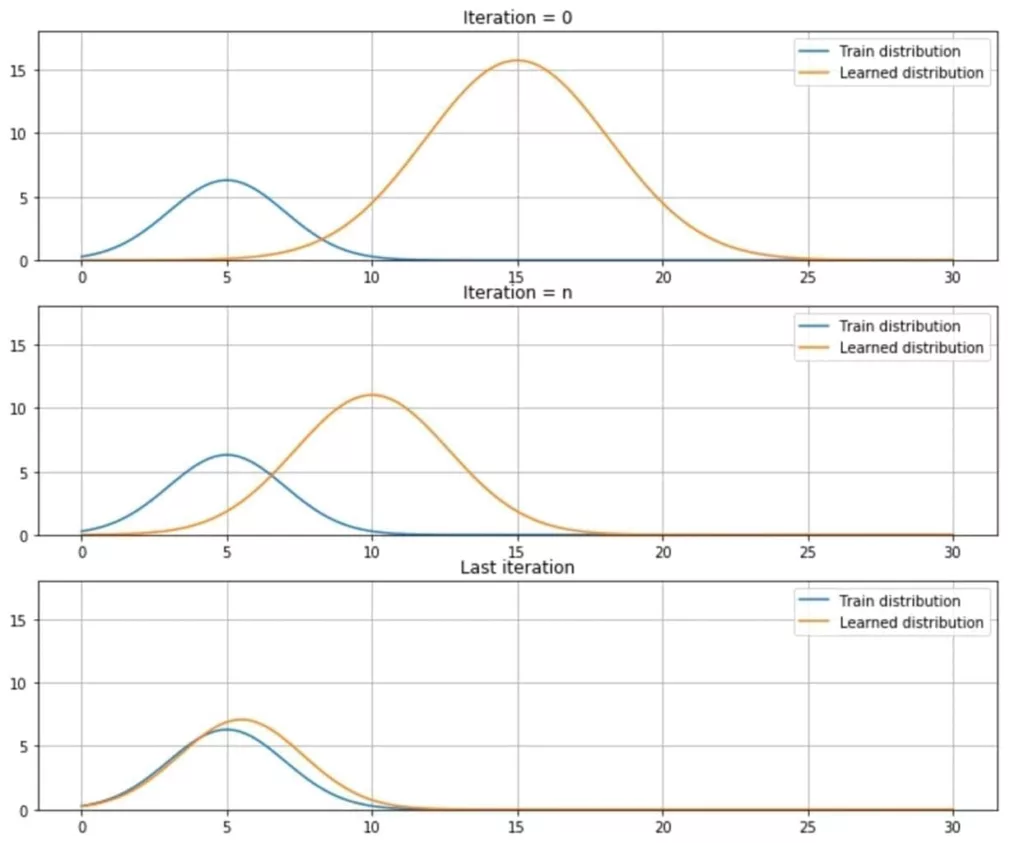
Therefore, the training process will “remodel” q(x) in order to minimize its divergence from p(x). In the following figure, there’s a schematic representation of this process before the initial iteration, at iteration n, and at the end of the training process:
If we consider, the mutual information between p(x) and q(x), we obtain:
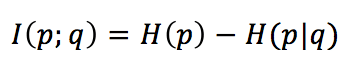
The mutual information is the amount of information shared by both distributions. It is expressed as the entropy of the training distribution minus the “unresolved” uncertainty that q provides when chosen instead of p. In other words, if we have modeled q perfectly, it means that q = p; therefore, H(q|q) = 0 and I(p;q) = H(p) (that represents the maximum amount of information that we can learn). Therefore, when we minimize the cross-entropy, we implicitly minimize the conditional entropy H(p|q), maximizing the mutual information.
An excellent introductory book on Information Theory:
If you like this post, you can always donate to support my activity! One coffee is enough!


