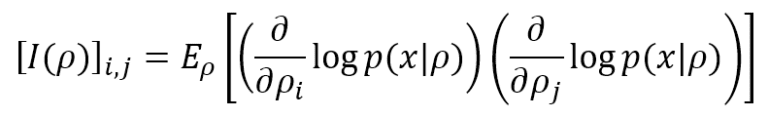Fisher Information, che prende il nome dallo statistico Ronald Fisher, è un potente strumento di statistica bayesiana e di apprendimento automatico. Per capire il suo significato ‘filosofico’, è utile pensare a un semplice compito di classificazione, dove il nostro compito è trovare un modello (caratterizzato da un insieme di parametri) che sia in grado di riprodurre il processo di generazione dei dati p(x) (normalmente rappresentato come un insieme di dati) con la massima precisione possibile. Questa condizione può essere espressa utilizzando la divergenza di Kullback-Leibler:
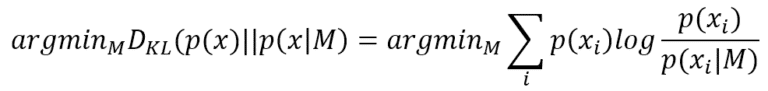
Trovare i migliori parametri che minimizzano la divergenza di Kullback-Leibler è equivalente a massimizzare il log-likelihood log P(x|M), perché p(x) non contiene alcun riferimento a M. Ora, una buona domanda (informale) è: quante informazioni può fornire p(x) per semplificare il compito al modello? In altre parole, data una log-likelihood, qual è il suo comportamento vicino al punto MLE?
Considerando i due grafici seguenti, possiamo osservare due situazioni diverse. La prima è una verosimiglianza molto alta, dove la probabilità di qualsiasi valore di parametro lontano dal MLE è quasi vicina allo zero. Nel secondo grafico, la curva è più piatta e p(MLE) è molto vicino a molti stati non ottimali.
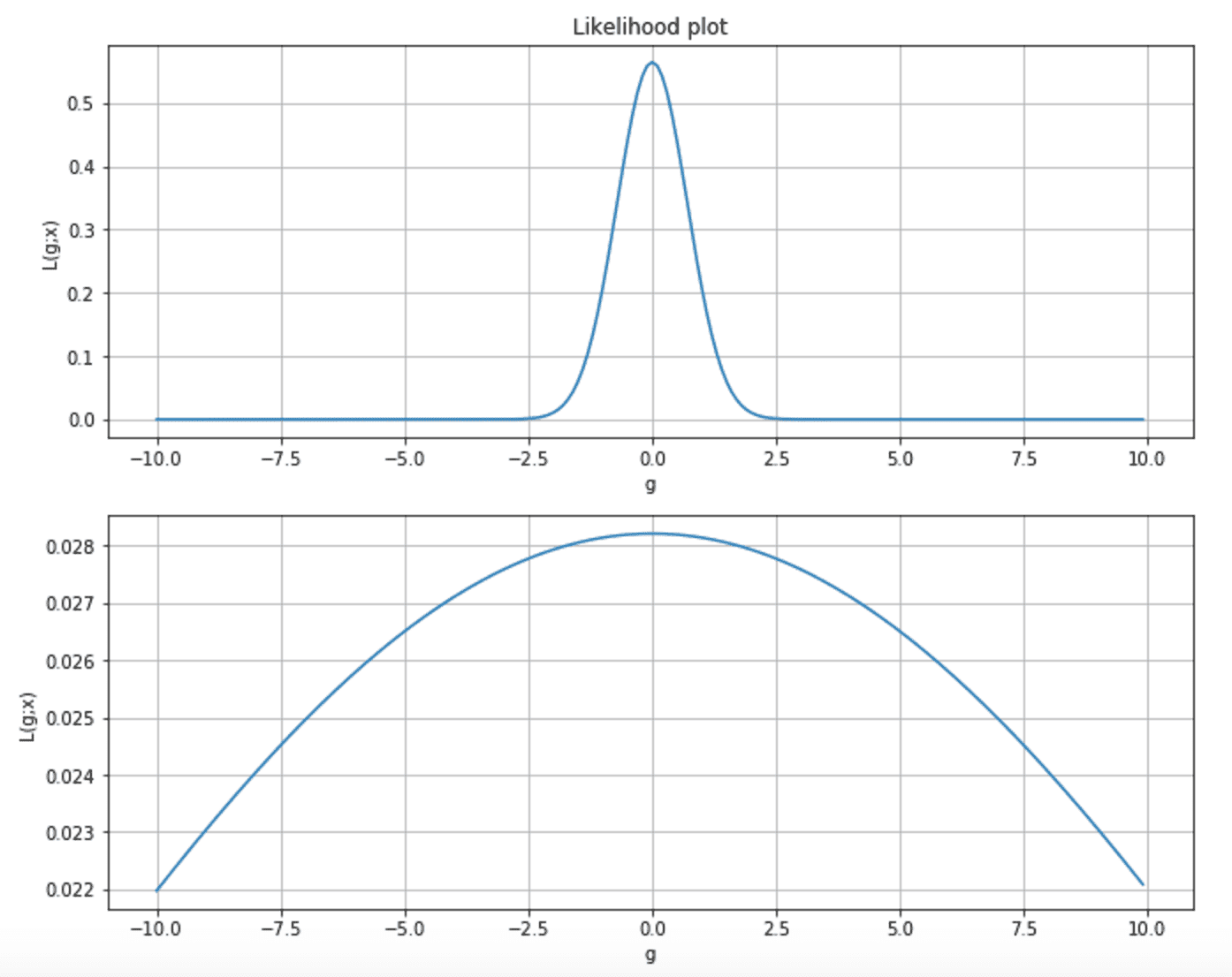
Inoltre, poiché la maggior parte delle tecniche di apprendimento si basa sul gradiente, nel primo caso, la sua grandezza è molto vicina al MLE, mentre, nel secondo, la velocità del gradiente è molto lenta e il processo di apprendimento può richiedere molto tempo per raggiungere il massimo.
L’informazione di Fisher aiuta a determinare il picco della funzione di verosimiglianza e fornisce una misura precisa della quantità di informazioni che il processo di generazione dei dati p(x) può fornire a M per raggiungere il MLE. La definizione più semplice si basa su un singolo parametro ρ. In forma discreta (più comune nell’apprendimento automatico), è equivalente a:
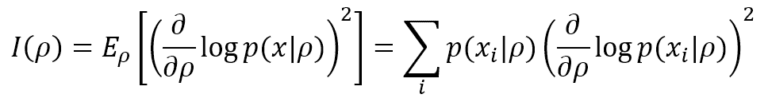
Il limite inferiore è 0, il che significa che non vengono fornite informazioni, mentre non esiste un limite superiore (+∞). Se il modello, come spesso accade, ha molti parametri (ρ1, ρ2, …, ρN), è possibile calcolare la Matrice informativa di Fisher, definita come:
In alcune condizioni di regolarità, è possibile trasformare entrambe le espressioni utilizzando le seconde derivate (molto spesso, la Matrice di Informazione di Fisher) viene calcolata come Hessiano negativo). Tuttavia, preferisco mantenere le espressioni originali, perché possono sempre essere applicate senza particolari restrizioni. Anche se, senza le seconde derivate esplicite, l’Informazione di Fisher fornisce una “velocità” del gradiente calcolato per ogni parametro. Più veloce è, più facile è il processo di apprendimento.
Ora, supponiamo di stimare il valore di un parametro ρ, attraverso un’approssimazione ρ′. Se E[ρ′] = ρ, lo stimatore è definito imparziale e l’unico elemento statistico da considerare è la varianza. Se il valore atteso è corretto, ma la varianza è molto alta, anche la probabilità di un valore sbagliato è molto alta. Pertanto, nell’apprendimento automatico, siamo interessati a conoscere la varianza minima di uno stimatore imparziale. Il limite di Cramér-Rao afferma che:
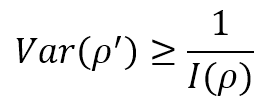
Pertanto, un’elevata Informazione di Fisher implica un limite inferiore di varianza, mentre una bassa Informazione di Fisher limita il nostro modello imponendo un’elevata varianza minima ottenibile. Naturalmente, questo non significa che ogni stimatore imparziale possa raggiungere il limite di Cramér-Rao, ma ci fornisce una misura della precisione massima teorica che possiamo raggiungere se il nostro modello è abbastanza potente.
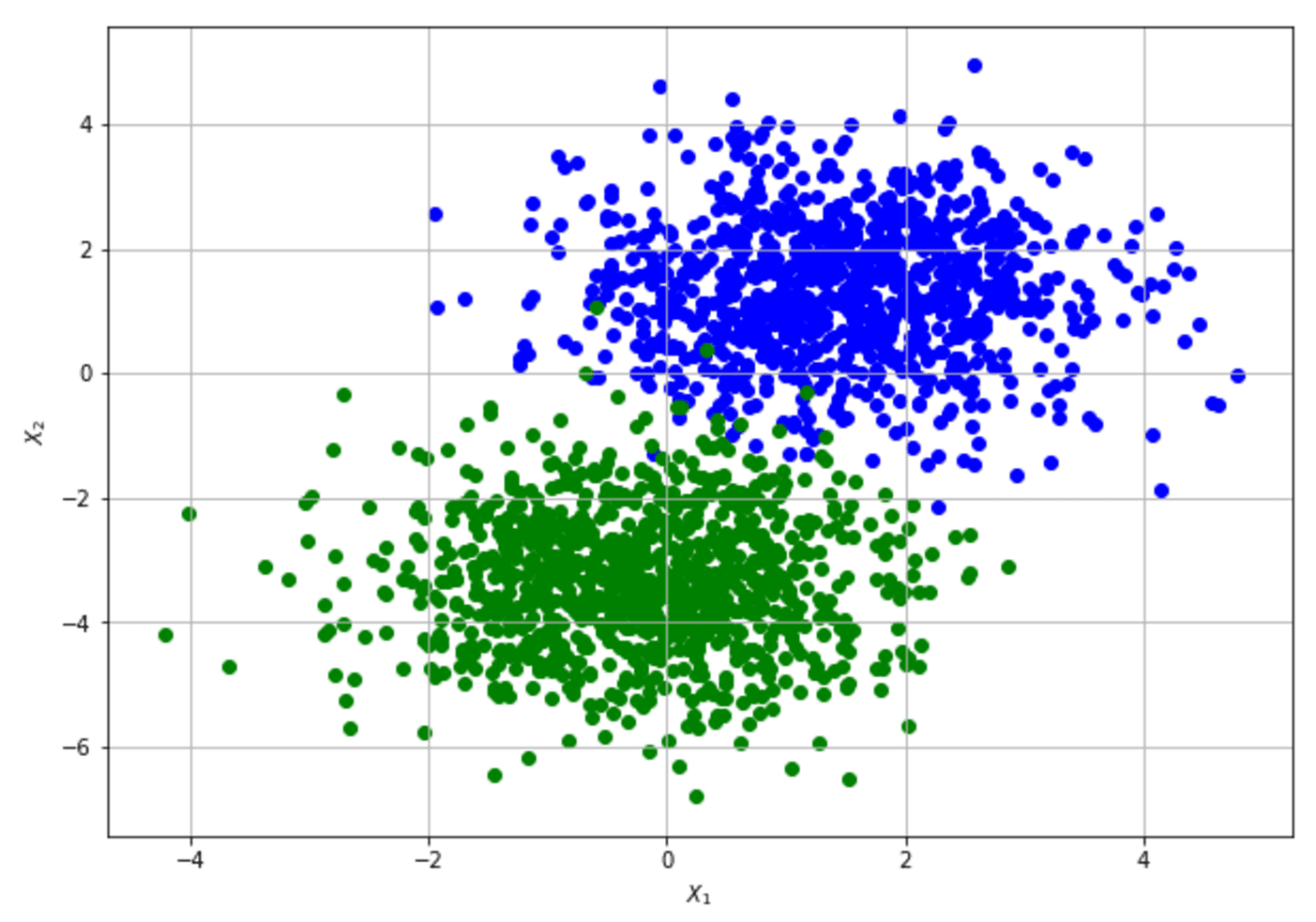
Per mostrare come calcolare la matrice informativa di Fisher e applicare il limite di Cramér-Rao, consideriamo un set di dati molto semplice (il nostro processo di generazione dei dati) che una Regressione Logistica può facilmente imparare:
Per semplicità, il set di dati 2D è stato modificato aggiungendo una colonna “ones” per apprendere il pregiudizio come qualsiasi altro peso. L’implementazione si basa su Tensorflow (disponibile su questo GIST), che consente un calcolo del gradiente numericamente stabile:
import numpy as np
import tensorflow as tf
from sklearn.datasets import make_blobs
# Set random seed (for reproducibility)
np.random.seed(1000)
# Create dataset
nb_samples=2000
X, Y = make_blobs(n_samples=nb_samples, n_features=2, centers=2, cluster_std=1.1, random_state=2000)
# Transform the original dataset so to learn the bias as any other parameter
Xc = np.ones((nb_samples, X.shape[1] + 1), dtype=np.float32)
Yc = np.zeros((nb_samples, 1), dtype=np.float32)
Xc[:, 1:3] = X
Yc[:, 0] = Y
# Create Tensorflow graph
graph = tf.Graph()
with graph.as_default():
Xi = tf.placeholder(tf.float32, Xc.shape)
Yi = tf.placeholder(tf.float32, Yc.shape)
# Weights (+ bias)
W = tf.Variable(tf.random_normal([Xc.shape[1], 1], 0.0, 0.01))
# Z = wx + b
Z = tf.matmul(Xi, W)
# Log-likelihood
log_likelihood = tf.reduce_sum(tf.nn.sigmoid_cross_entropy_with_logits(logits=Z, labels=Yi))
# Cost function (Log-likelihood + L2 penalty)
cost = log_likelihood + 0.5*tf.norm(W, ord=2)
trainer = tf.train.GradientDescentOptimizer(0.000025)
training_step = trainer.minimize(cost)
# Compute the FIM
dW = tf.gradients(-log_likelihood, W)
FIM = tf.matmul(tf.reshape(dW, (Xc.shape[1], 1)), tf.reshape(dW, (Xc.shape[1], 1)), transpose_b=True)
# Create Tensorflow session
session = tf.InteractiveSession(graph=graph)
# Initialize all variables
tf.global_variables_initializer().run()
# Run a training cycle
# The model is quite simple, however a check on the cost function should be performed
for _ in range(3500):
_, _ = session.run([training_step, cost], feed_dict={Xi: Xc, Yi: Yc})
# Compute Fisher Information Matrix on MLE
fisher_information_matrix = session.run([FIM], feed_dict={Xi: Xc, Yi: Yc})
La matrice informativa di Fisher risultante è:
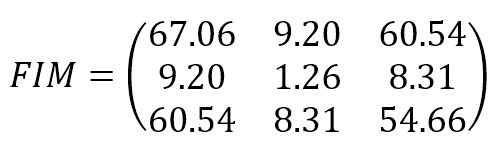
I parametri sono (bias, w1, w2). Il risultato mostra che il set di dati originali fornisce un’informazione abbastanza elevata nella stima del bias e di w2 e un’informazione più bassa nella stima di w1. Il limite di Cramér-Rao stabilisce una varianza minima molto piccola per bias e w2 e un valore relativamente più alto per w1. Dalla struttura del set di dati si può ricavare un’interpretazione di questo risultato: muovendosi lungo l’asse x2, è facile trovare un confine che separa i punti blu e verdi; d’altra parte, questo non è vero quando si esplora la prima dimensione. Al contrario, nessuno dei valori FIM è 0 (o molto vicino a 0), il che significa che i parametri non sono ortogonali e non possono essere appresi separatamente.
Se si vuole ottenere un’espressione FIM analitica, è necessario considerare tutti i valori possibili (o un ampio insieme) e calcolare il valore atteso facendo una media su ρ.
Per una comprensione più approfondita dell’Informazione di Fisher, può vedere questa lezione su YouTube:
Se ti piace l’articolo, puoi sempre fare una donazione per supportare la mia attività. Basta un caffè!