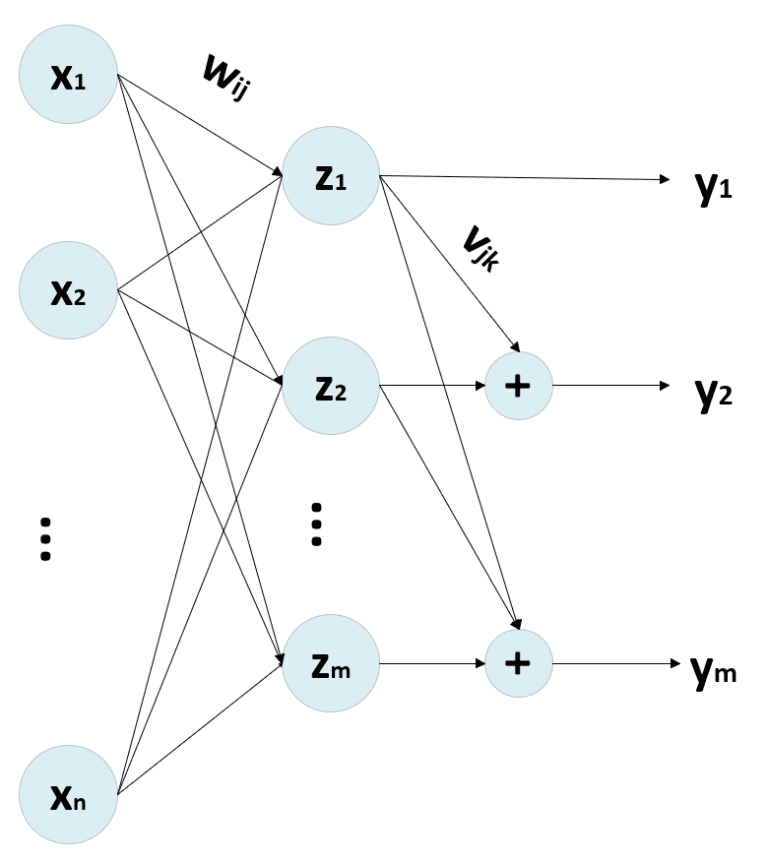
Uno degli effetti più interessanti della PCA (Analisi delle Componenti Principali) è quello di decorrelare la matrice di covarianza C dell’ingresso, calcolando gli autovalori e operando un cambiamento di base con una matrice V:
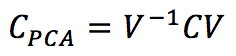
Gli autovalori sono ordinati in ordine decrescente, considerando l’autovalore corrispondente. Pertanto, Cpca è una matrice diagonale in cui gli elementi non nulli sono λ1 >= λ2 >= λ3 >= … >= λn. Selezionando i p autovalori superiori, è possibile operare una riduzione della dimensionalità proiettando i campioni nel nuovo sottospazio determinato dai p autovalori superiori (è possibile utilizzare l’ortonormalizzazione di Gram-Schmidt se non hanno una lunghezza unitaria). La procedura PCA standard funziona con un approccio bottom-up, ottenendo la decorrelazione di C come effetto finale. Tuttavia, è possibile impiegare le reti neurali, imponendo questa condizione come fase di ottimizzazione. Uno dei modelli più efficaci è stato proposto da Rubner e Tavan (e prende il nome da loro). La sua struttura generica è:
Se supponiamo che N (dimensionalità di ingresso) << M (dimensionalità di uscita), l’uscita della rete può essere calcolata come segue:
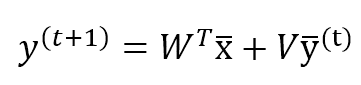
Dove V (n × n) è una matrice triangolare inferiore con tutti gli elementi diagonali a 0, e W ha una forma (n × m). Inoltre, è necessario memorizzare la y(t) per poter calcolare la y(t+1). Questa procedura deve essere ripetuta fino alla stabilizzazione del vettore di uscita. In genere, dopo k < 10 iterazioni, le modifiche sono inferiori alla soglia di 0,0001. Tuttavia, è importante verificare questo valore in ogni applicazione reale.
Il processo di formazione viene gestito con due regole di aggiornamento:
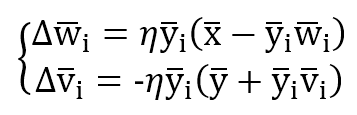
Il primo è Hebbiano basato sulla regola di Oja, mentre il secondo è anti-Hebbian perché il suo scopo è ridurre la correlazione tra le unità di uscita. Infatti, senza il fattore di normalizzazione, l’aggiornamento è nella forma dW = -αy(i)y(k) per ridurre il peso sinaptico quando due unità di uscita sono correlate (stesso segno).
Se la matrice V viene mantenuta triangolare superiore, è possibile vettorializzare il processo. Esistono anche altre varianti, come la rete Földiák, che adotta una matrice V simmetrica per aggiungere il contributo di tutte le altre unità a y(i). Tuttavia, il modello di Rubner-Tavan sembra più simile al processo adottato in una PCA sequenziale, dove il secondo componente viene calcolato come ortogonale al primo e così via fino all’ultimo.
Il codice di esempio si basa sul set di dati MNIST fornito da Scikit-Learn e adotta un numero fisso di cicli per stabilizzare l’uscita. Il codice è disponibile anche in questo GIST:
from sklearn.datasets import load_digits
import numpy as np
# Set random seed for reproducibility
np.random.seed(1000)
# Load MNIST dataset
X, Y = load_digits(return_X_y=True)
X /= 255.0
n_components = 16
learning_rate = 0.001
epochs = 20
stabilization_cycles = 5
# Weight matrices
W = np.random.uniform(-0.01, 0.01, size=(X.shape[1], n_components))
V = np.triu(np.random.uniform(-0.01, 0.01, size=(n_components, n_components)))
np.fill_diagonal(V, 0.0)
# Training process
for e in range(epochs):
for i in range(X.shape[0]):
y_p = np.zeros((n_components, 1))
xi = np.expand_dims(Xs[i], 1)
for _ in range(stabilization_cycles):
y = np.dot(W.T, xi) + np.dot(V, y_p)
y_p = y.copy()
dW = np.zeros((X.shape[1], n_components))
dV = np.zeros((n_components, n_components))
for t in range(n_components):
y2 = np.power(y[t], 2)
dW[:, t] = np.squeeze((y[t] * xi) + (y2 * np.expand_dims(W[:, t], 1)))
dV[t, :] = -np.squeeze((y[t] * y) + (y2 * np.expand_dims(V[t, :], 1)))
W += (learning_rate * dW)
V += (learning_rate * dV)
V = np.tril(V)
np.fill_diagonal(V, 0.0)
W /= np.linalg.norm(W, axis=0).reshape((1, n_components))
# Compute all output components
Y_comp = np.zeros((X.shape[0], n_components))
for i in range(X.shape[0]):
y_p = np.zeros((n_components,))
xi = np.expand_dims(Xs[i], 1)
for _ in range(stabilization_cycles):
Y_comp[i] = np.squeeze(np.dot(W.T, xi) + np.dot(V.T, y_p))
y_p = y.copy()
Se ti piace l’articolo, puoi sempre fare una donazione per supportare la mia attività. Basta un caffè!