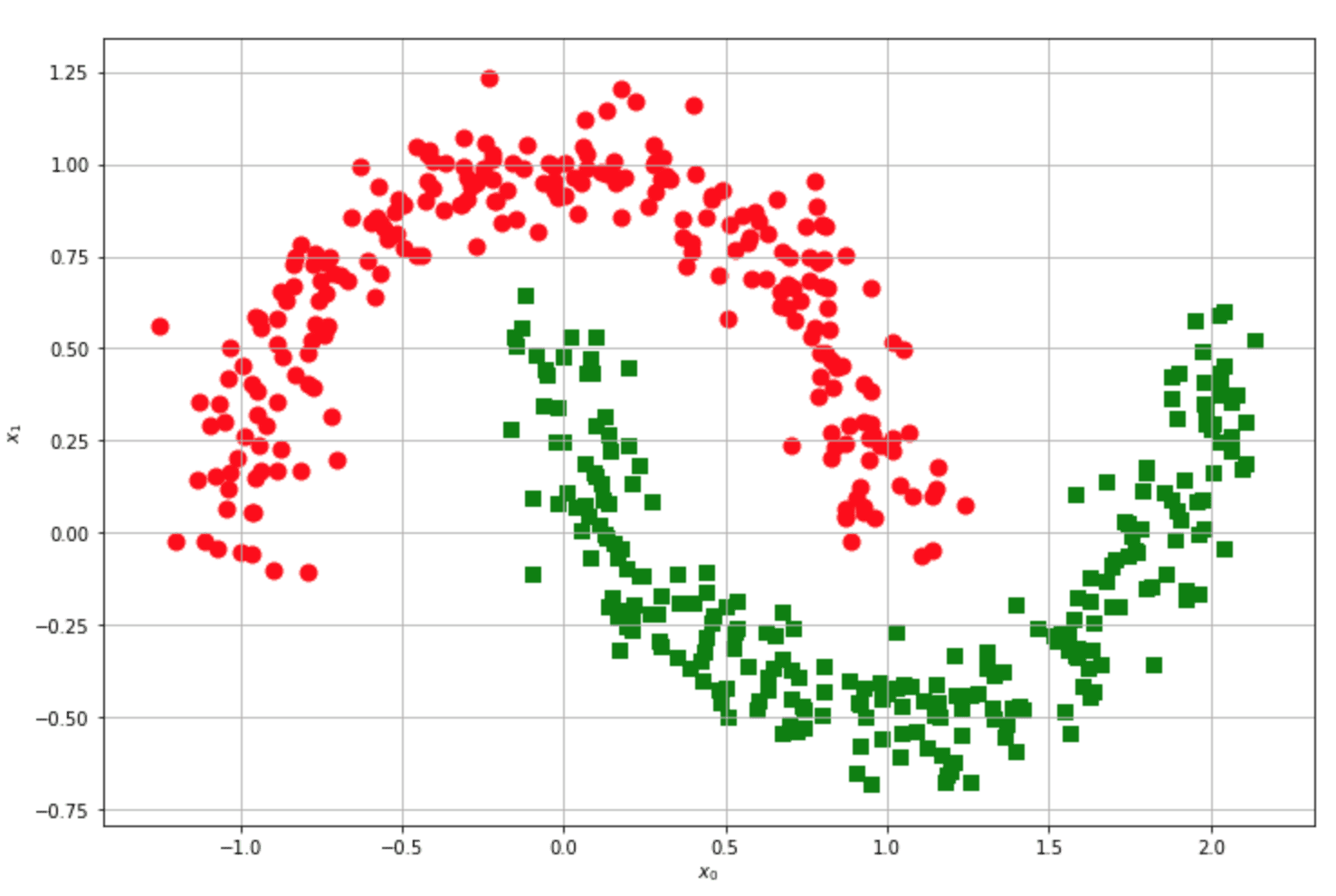
Si tratta di un’introduzione rapida ai metodi kernel e la cosa migliore da fare è iniziare con una domanda molto semplice. Questo insieme bidimensionale è linearmente separabile?
Naturalmente, la risposta è sì, lo è. Perché? Un insieme di dati definito in un sottospazio Ω ⊆ ℜn è linearmente separabile se esiste un’ipersuperficie (n-1)-dimensionale in grado di separare tutti i punti appartenenti a una classe dagli altri. Consideriamo il problema da un altro punto di vista, supponendo, per semplicità, di lavorare in 2D.
Abbiamo definito un’ipotetica linea di separazione e impostato un punto arbitrario O come origine. Disegniamo ora il vettore w, ortogonale alla linea, e puntiamo in uno dei due sottospazi. Consideriamo ora il prodotto interno tra w e un punto casuale x0: come possiamo decidere se si trova sul lato puntato da w? In parole povere, il prodotto interno è proporzionale al coseno dell’angolo tra i due vettori. Se tale angolo è compreso tra -π/2 e π/2, il coseno è non negativo, altrimenti è non positivo:
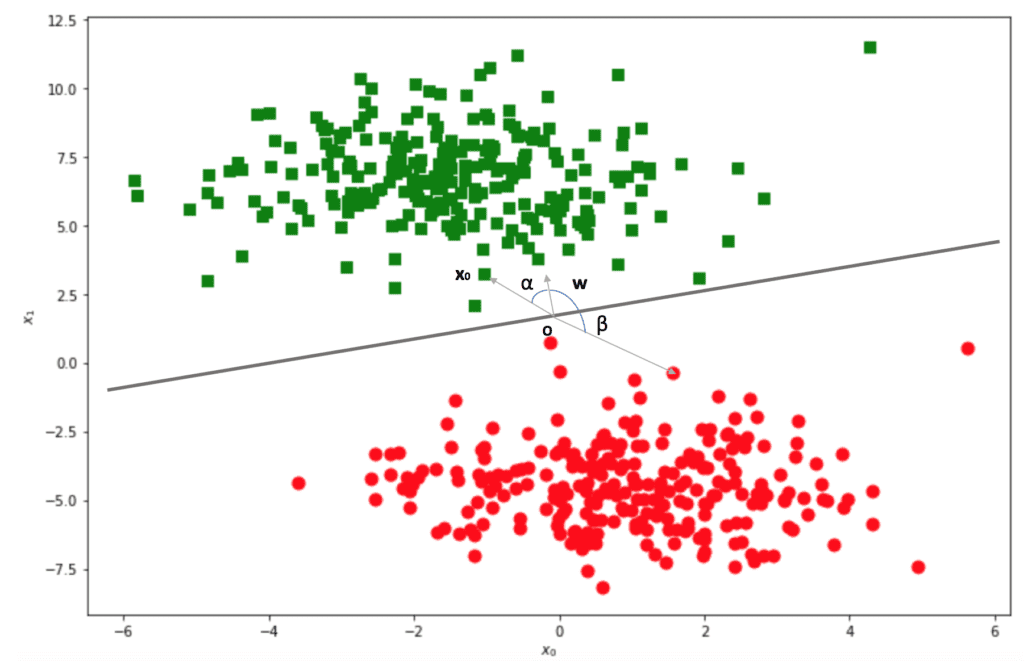
Si tratta di dimostrare che tutti gli angoli α tra w e i punti verdi sono sempre delimitati tra -π/2 e π/2. Pertanto, tutti i prodotti interni sono positivi (non ci sono punti sulla linea in cui il coseno è 0). Allo stesso tempo, tutti gli angoli β sono delimitati tra π/2 e 3π/2 dove il coseno è negativo.
Ora, dovrebbe essere ovvio che w è il vettore dei pesi di un classificatore lineare ‘puro’ (come un Perceptron), e la regola decisionale corrispondente è:
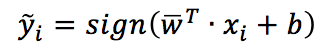
Il modo di determinare w cambia a seconda dell’algoritmo, così come la regola decisionale, che è sempre una funzione strettamente legata all’angolo tra w e il campione.
Consideriamo ora un altro esempio famoso:
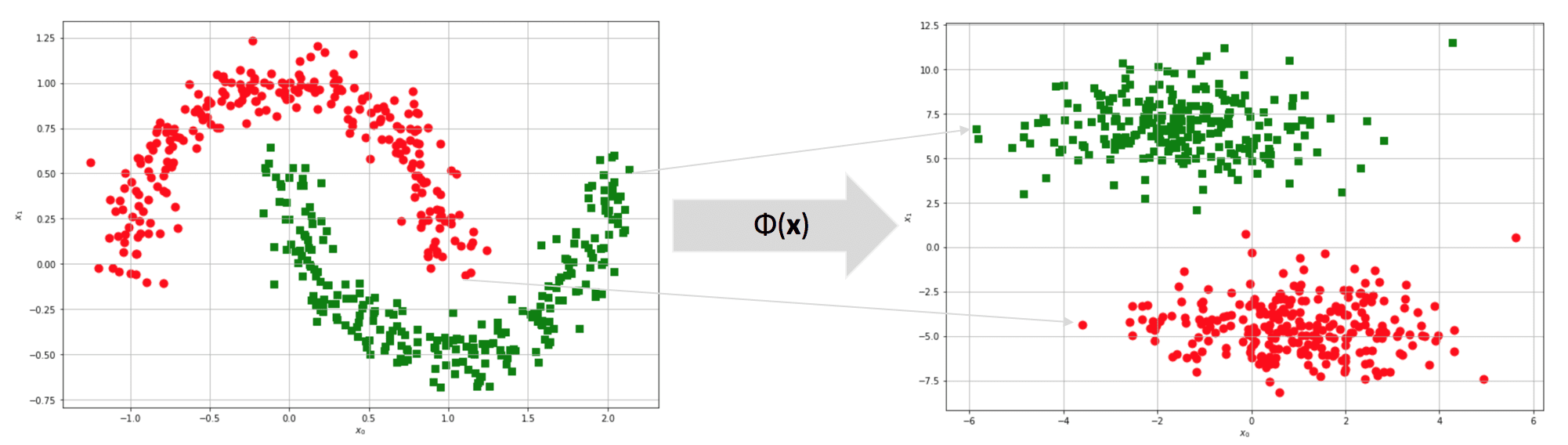
Questo set di dati è linearmente separabile? È libero di provarci, ma la risposta è no. Per ogni linea tracciata, i punti rossi e verdi si troveranno sempre sullo stesso lato, quindi la precisione non potrà mai superare una soglia fissa (piuttosto bassa). Ora, supponiamo di proteggere il set di dati originale in uno spazio di caratteristiche m-dimensionale (m può anche essere uguale a n):
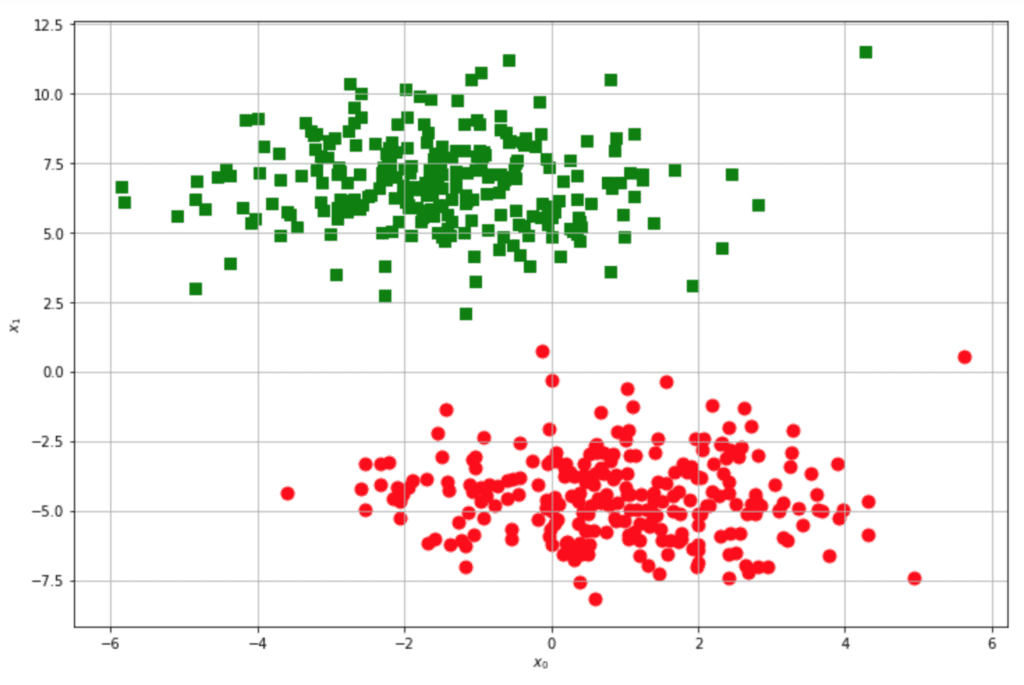
Dopo la trasformazione, il set di dati originale della mezza luna diventa linearmente separabile! Tuttavia, c’è ancora un problema: abbiamo bisogno di un classificatore che lavori nello spazio originale per calcolare un prodotto interno di punti trasformati. Analizziamo il problema utilizzando le SVM (Support Vector Machines), dove i kernel sono molto diffusi. Un algoritmo SVM cerca di massimizzare la separazione tra i blocchi ad alta densità. Non mi occupo di tutti i dettagli (che si possono trovare in tutti i libri di apprendimento automatico), ma devo definire l’espressione per i pesi:
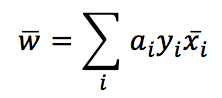
Non è importante se non si sa come vengono ricavati. È più semplice capire il risultato finale: se si riconsidera l’immagine mostrata prima, dove avevamo tracciato una linea di separazione, tutti i punti verdi hanno y=1. Pertanto, w è la somma ponderata di tutti i campioni. I valori di αi si ottengono attraverso il processo di ottimizzazione; tuttavia, alla fine, dovremmo osservare un w simile a quello che abbiamo arbitrariamente disegnato.
Se dobbiamo passare allo spazio delle caratteristiche, ogni x deve essere filtrato da φ(x). Pertanto, otteniamo:
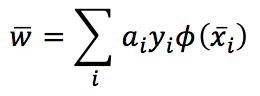
La funzione decisionale corrispondente diventa:
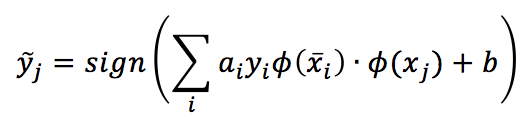
Poiché la somma è estesa a tutti i campioni, dobbiamo calcolare N prodotti interni di campioni trasformati. Non si tratta di una soluzione rapida e adeguata! Tuttavia, ci sono funzioni particolari chiamate kernel, che hanno una proprietà molto bella:
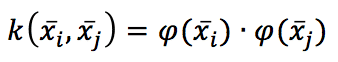
In altre parole, il kernel, valutato su xi, xj, equivale al prodotto interno dei due punti proiettati da una funzione ρ(x). Attenzione: ρ è un’altra funzione perché, se partiamo dalla proiezione, non saremo in grado di trovare un kernel, mentre se partiamo dal kernel, c’è anche un famoso risultato matematico (Teorema di Mercer) che garantisce, dato un kernel continuo, simmetrico e (semi)definito positivo, l’esistenza di una trasformazione implicita ρ(x) sotto alcune condizioni (facilmente soddisfatte).
Non è difficile capire che, utilizzando un kernel, la funzione decisionale diventa:
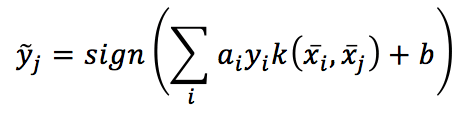
Che è molto più facile da valutare.
In teoria, potremmo cercare di trovare un kernel per una trasformazione specifica, ma nella vita reale, solo alcuni kernel sono utili in molti contesti diversi. Ad esempio, la Funzione Base Radiale:
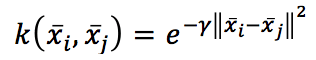
Il che è eccellente quando dobbiamo rimappare lo spazio originale in uno spazio radiale. O il kernel polinomiale:
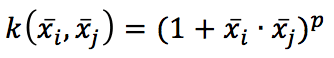
Che determina tutte le caratteristiche dei termini polinomiali (come x2 o 2 xixj). Esistono anche altri kernel, come sigmoid o tanh, ma iniziare con un classificatore lineare è sempre una buona idea. Se la precisione è troppo bassa, è possibile provare un kernel RBF o polinomiale, poi altre varianti, e se non funziona nulla, probabilmente è necessario cambiare il modello!
I kernel non si limitano ai classificatori: possono essere impiegati nella PCA (la Kernel PCA permette di estrarre le componenti principali da insiemi di dati non lineari e da algoritmi di apprendimento basati sulle istanze. Il principio è sempre lo stesso (ed è la pallottola d’argento del kernel: rappresenta il prodotto interno di proiezioni non lineari che possono rimappare il set di dati originale in uno spazio dimensionale superiore, dove è più facile trovare una soluzione lineare).
Se ti piace l’articolo, puoi sempre fare una donazione per supportare la mia attività. Basta un caffè!