Many clustering algorithms must define the number of desired clusters before fitting the model. This requirement can appear as a contradiction in an unsupervised scenario. However, in real-world scenarios, data science often already knows about a reasonable range of clusters. Unfortunately, this doesn’t imply being able to define the optimal number of clusters without further analysis.
Cluster instability analysis is a powerful tool to assess the optimality of a specific algorithm or configuration. The idea, developed in [1], is simple and can be easily understood using a mechanical analogy. If we have some balls on a table, we want to group them so that small perturbations (movements) cannot alter the initial cluster assignment. For example, if two groups are very close, a perturbation can push a ball into another cluster, as shown in the following figure:
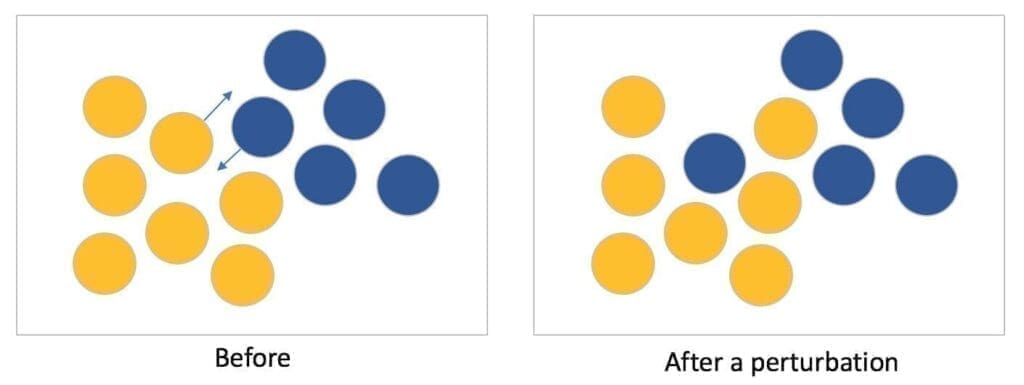
More formally, if we consider a clustering function C(X) and an original dataset X, we can create n perturbed versions of X (for example, adding noise or subsampling):
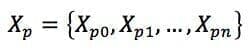
Considering a distance metric function d(X, Y) between two clusterings (Euclidean, Hamming, and so on), it’s possible to define the instability as:
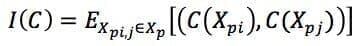
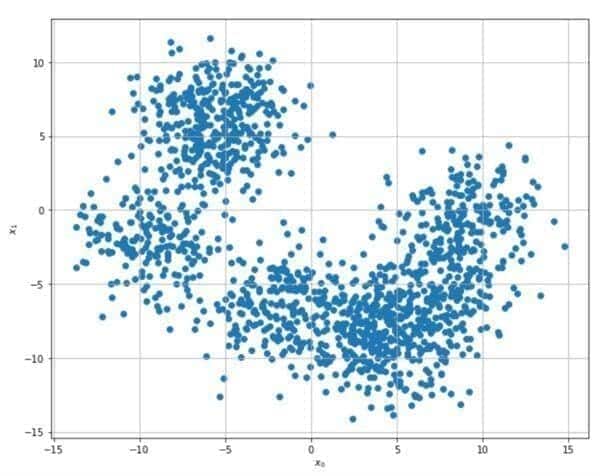
The following example is based on the Scikit-Learn and K-Means algorithm. The original dataset (generated using the make_blobs function) is shown in the following figure:
To test the stability, 20 noisy versions are generated, and the process is repeated for a number of clusters between 2 and 15 using the normalized Hamming distance:
The corresponding plot is:
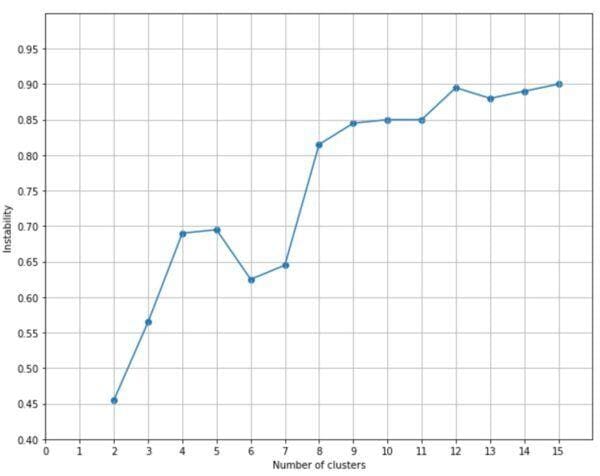
If we exclude 2 and 3 clusters, a good solution seems to be offered by n=6, where the instability has a local minimum. Greater values are not acceptable because the instability increases over an acceptable threshold. After all, considering the initial distribution, it’s easy to understand that many clusters (for example, 15) drive to very close groups, where a perturbation can dramatically alter the configuration, pushing too many points into a different cluster.
Picking n=6, a default Scikit-Learn K-Means produces the following result:
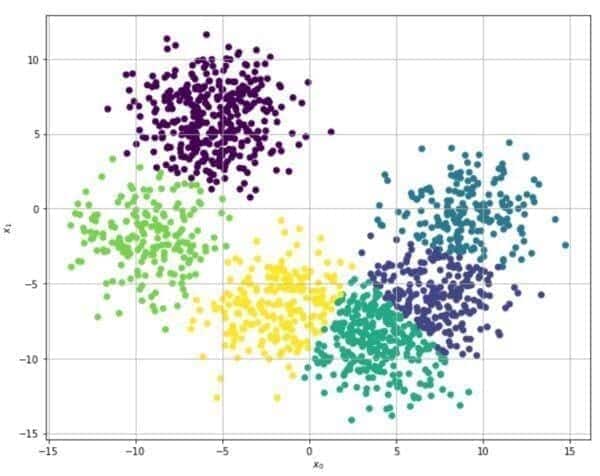
The clustering appears reasonable, and the blocks show good internal cohesion even if the inter-cluster separation is not very high (due to the original distribution, which is quite dense).
References:
-
- Von Luxburg U., Cluster stability: an overview, arXiv 1007:1075v1
If you like this post, you can always donate to support my activity! One coffee is enough!

