Le mappe auto-organizzanti (SOM) sono strutture neurali proposte per la prima volta dall’informatico T. Kohonen alla fine degli anni ’80 (per questo sono note anche come Reti Kohonen). Le loro peculiarità sono la capacità di auto-clusterizzare i dati in base alle caratteristiche topologiche dei campioni e l’approccio al processo di apprendimento. A differenza di metodi come le Gaussian Mixtures o K-Means, una SOM apprende attraverso un processo di apprendimento competitivo . In altre parole, il modello cerca di specializzare i suoi neuroni in modo da essere in grado di produrre una risposta solo per una particolare famiglia di modelli (può anche trattarsi di un singolo campione di ingresso che rappresenta una famiglia, come una lettera scritta a mano).
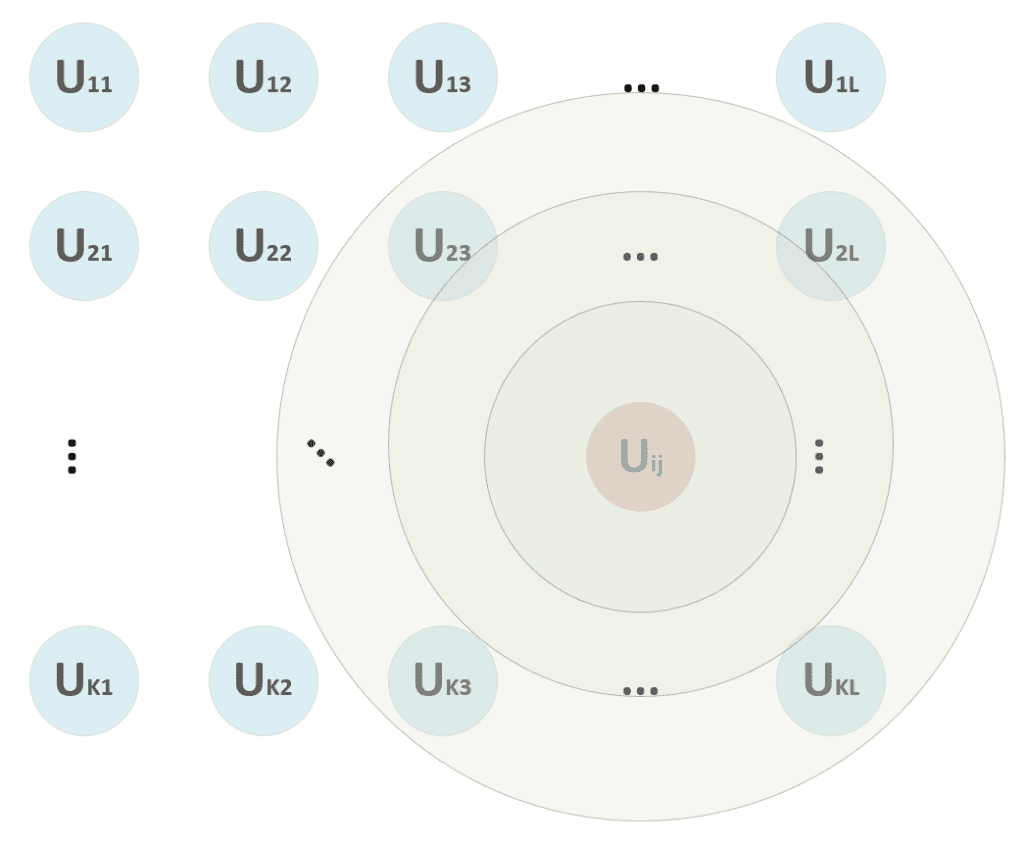
Consideriamo un set di dati contenente N campioni p-dimensionali. Una SOM adatta è una matrice (sono possibili anche altre forme, come i toroidi) contenente (K × L) recettori, ognuno dei quali comprende p pesi sinaptici. La struttura risultante è una matrice tridimensionale W con una forma (K × L × p).
Durante il processo di apprendimento, si estrae un campione x dalla distribuzione X che genera i dati e si calcola un’unità vincente come:
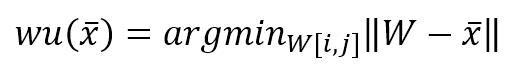
Nella formula precedente, ho adottato la notazione vettoriale. Il processo deve calcolare la distanza tra x e tutti i vettori p-dimensionali W[i, j], determinando la tupla (i, j) corrispondente all’unità che ha mostrato la massima attivazione (distanza minima). Una volta trovata l’unità vincente, deve essere calcolata una funzione di distanza. Consideriamo lo schema mostrato nella figura seguente:
All’inizio del processo di formazione, non siamo sicuri se l’unità vincente rimarrà la stessa. Pertanto, applichiamo l’aggiornamento a un quartiere centrato in (i, j) e con un raggio che diminuisce proporzionalmente all’epoca di addestramento. Nella figura, ad esempio, l’unità vincente può iniziare a considerare anche le unità (2, 3) → (2, L), …, (K, 3) → (K, L), ma, dopo alcune epoche, il raggio diventa 1, considerando solo (i, j) senza nessun altro vicino.
Questa funzione è rappresentata come una matrice (K × L) il cui elemento generico è:
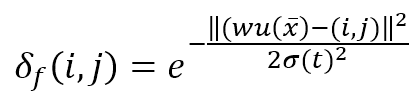
Il numeratore dell’esponenziale è la distanza euclidea tra l’unità vincente e il generico recettore (i, j). La distanza è controllata dal parametro σ(t), che dovrebbe diminuire (possibilmente in modo esponenziale) con il numero di epoche. Molti autori (come Floreano e Mattiussi, vedere il riferimento per ulteriori informazioni) suggeriscono di introdurre una costante temporale τ e di definire σ(t) come:
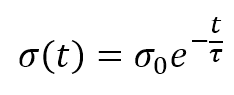
La regola di aggiornamento competitivo per i pesi è:
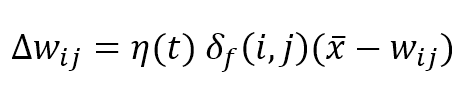
Dove η(t) è il tasso di apprendimento che può essere fisso (ad esempio η = 0,05) o decadente in modo esponenziale come σ(t), i pesi vengono aggiornati sommando il termine Δw:
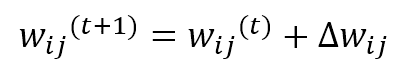
Come si può vedere, i pesi appartenenti al quartiere dell’unità vincente (determinati da δf) si avvicinano a x, mentre gli altri rimangono fissi (δf = 0). Il ruolo della funzione di distanza è quello di imporre un aggiornamento massimo (che deve produrre la risposta più forte) in prossimità dell’unità vincente e uno decrescente a tutte le altre unità. Nella figura seguente, c’è una rappresentazione bidimensionale di questo processo:
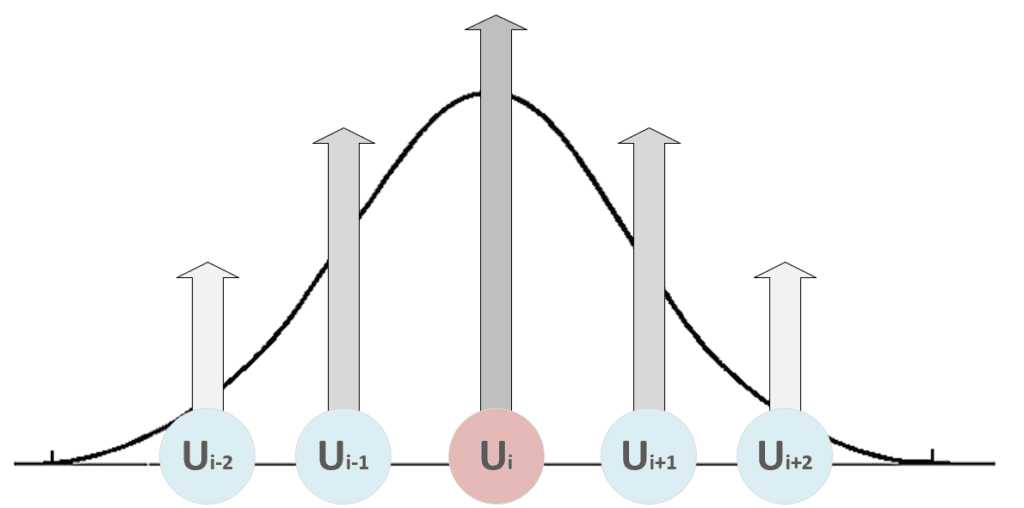
Tutte le unità con i < i-2 e i > i+2 sono fisse. Pertanto, quando la funzione di distanza diventa stretta in modo da includere solo l’unità vincente, si ottiene un principio di massima selettività attraverso un processo competitivo. Questa strategia è necessaria per consentire alla mappa di creare aree reattive nel modo più efficiente. Senza una funzione di distanza, la competizione non potrebbe avvenire affatto o, in alcuni casi, la stessa unità potrebbe essere attivata dagli stessi modelli, portando la rete a un ciclo infinito.
Anche se non forniamo alcuna prova, una rete Kohonen addestrata utilizzando una funzione di distanza decrescente convergerà verso uno stato stabile se la matrice (K × L) è abbastanza grande. Suggerisco di provare matrici più piccole (ma con KL > N) e di aumentare le dimensioni fino a raggiungere il risultato desiderato. Purtroppo, però, il processo è piuttosto lento e la convergenza viene normalmente raggiunta dopo migliaia di iterazioni dell’intero set di dati. Per questo motivo, spesso è preferibile ridurre la dimensionalità (tramite PCA, Kernel-PCA o NMF) e utilizzare un algoritmo di clustering standard.
Un elemento importante è l’inizializzazione di W. Non ci sono pratiche migliori. Tuttavia, se i pesi sono già vicini ai componenti più significativi della popolazione, la convergenza può essere più rapida. Una possibilità è quella di eseguire una decomposizione spettrale (come in una PCA) per determinare gli autovettori principali. Tuttavia, quando il set di dati presenta delle non linearità, questo processo è quasi inutile. Suggerisco di inizializzare i pesi campionando casualmente i valori da una distribuzione uniforme (min(X), max(X)) (X è il set di dati di ingresso). Un’altra possibilità è quella di provare diverse inizializzazioni, calcolando l’errore medio sull’intero set di dati e prendendo i valori che minimizzano questo errore (è utile provare a campionare da distribuzioni gaussiane e uniformi con un numero di prove superiore a 10). In generale, il campionamento da una distribuzione uniforme produce errori medi con una deviazione standard < 0,1. Pertanto, non ha senso provare troppe combinazioni.
Per testare la SOM, ho utilizzato i primi 100 volti del set di dati Olivetti(AT&T Laboratories Cambridge) forniti da Scikit-Learn. Ogni campione ha una lunghezza di 4096 float [0, 1] (corrispondenti a 64 × 64 immagini in scala di grigi). Ho utilizzato una matrice con forma (20 × 20), 5000 iterazioni, utilizzando una funzione di distanza con σ(0) = 10 e τ = 400 per le prime 100 iterazioni e fissando i valori σ = 0,01 e η = 0,1 ÷ 0,5 per le restanti. Per accelerare i calcoli dei blocchi, ho deciso di utilizzare Cupy, che funziona come NumPy ma sfrutta la GPU (è possibile passare a NumPy semplicemente cambiando l’importazione e utilizzando lo spazio dei nomi np invece di cp). Purtroppo, ci sono molti cicli ed è difficile parallelizzare tutte le operazioni. Il codice è disponibile in questo GIST:
import cupy as cp
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import fetch_olivetti_faces
# Set random seed for reproducibility
np.random.seed(1000)
cp.random.seed(1000)
# Retrieve the dataset
faces = fetch_olivetti_faces()
nb_iterations = 5000
nb_startup_iterations = 100
nb_patterns = 100
pattern_length = faces['data'].shape[1]
pattern_width = pattern_height = int(np.sqrt(pattern_length))
eta0 = 1.0
sigma0 = 10
tau = 400.0
matrix_side = 20
precomputed_distances = np.zeros((matrix_side, matrix_side, matrix_side, matrix_side))
# Create the training set
X = faces['data']
X_train = cp.array(X[0:nb_patterns])
# Initialize the weights
W = cp.random.uniform(cp.min(X_train), cp.max(X_train), size=(matrix_side, matrix_side, pattern_length))
def winning_unit(xt):
distances = cp.linalg.norm(W - xt, ord=2, axis=2)
max_activation_unit = cp.argmax(distances)
return int(cp.floor(max_activation_unit / matrix_side)), max_activation_unit % matrix_side
def eta(t):
return eta0 * cp.exp(-float(t) / tau)
def sigma(t):
return float(sigma0) * cp.exp(-float(t) / tau)
# Precompute the distances
for i in range(matrix_side):
for j in range(matrix_side):
for k in range(matrix_side):
for t in range(matrix_side):
precomputed_distances[i, j, k, t] = np.power(float(i) - float(k), 2) + np.power(float(j) - float(t), 2)
precomputed_distances = cp.array(precomputed_distances)
def distance_matrix(xt, yt, sigmat):
dm = precomputed_distances[xt, yt, :, :]
de = 2.0 * cp.power(sigmat, 2)
return cp.exp(-dm / de)
if __name__ == '__main__':
# Main cycle
sequence = np.arange(0, nb_patterns)
for t in range(nb_iterations):
np.random.shuffle(sequence)
if t < nb_startup_iterations:
etat = eta(t)
sigmat = sigma(t)
else:
etat = 0.1
sigmat = 0.01
for n in sequence:
x_sample = X_train[n]
xw, yw = winning_unit(x_sample)
dm = distance_matrix(xw, yw, sigmat)
dW = etat * cp.expand_dims(dm, axis=2) * (x_sample - W)
W += dW
# Show the weight matrix
matrix_w = cp.zeros((matrix_side * pattern_height, matrix_side * pattern_width))
for i in range(matrix_side):
for j in range(matrix_side):
matrix_w[i * pattern_height:i * pattern_height + pattern_height,
j * pattern_height:j * pattern_height + pattern_width] = W[i, j].reshape((pattern_height, pattern_width)) * 255.0
fig, ax = plt.subplots(figsize=(12, 12))
ax.matshow(matrix_w.tolist(), cmap='gray')
ax.set_xticks([])
ax.set_yticks([])
plt.show()
La matrice con i vettori di peso rimodellati come immagini quadrate (come i campioni originali) è mostrata nella figura seguente:

Un lettore attento può notare leggere differenze tra i volti (negli occhi, nel naso, nella bocca e nelle sopracciglia). Le facce più definite corrispondono alle unità vincenti, mentre le altre sono vicine. Consideriamo che ognuno di essi è un peso sinaptico che deve corrispondere a un modello specifico. Possiamo pensare a questi vettori come a pseudo autogeni come nella PCA, anche se l’apprendimento competitivo cerca di trovare i valori che minimizzano la distanza euclidea, quindi l’obiettivo non è trovare componenti indipendenti. Poiché il set di dati è limitato a 100 campioni, non tutti i dettagli del viso sono stati inclusi nel set di formazione.
Riferimenti:
-
- Floreano D., Mattiussi C., Bio-Inspired Artificial Intelligence: Theories, Methods, and Technologies, The MIT Press
Se ti piace l’articolo, puoi sempre fare una donazione per supportare la mia attività. Basta un caffè!