Think about walking along a beach. The radio of a small kiosk bar is turned on, and a local DJ announces an 80s song. Immediately, the image of a car comes to your mind. It’s your first car, a second-hand blue spider. While listening to the same song, you drove your girlfriend to the beach about 25 years ago. It was the first time you made love to her. Now imagine a small animal (normally a prey, like a rodent) roaming around the forest and looking for food. A sound is suddenly heard, and the rodent raises its head. Is it the pounding of water or a lion’s roar? We can skip the answer right now. Let’s only think about the ways an animal’s memory can work.
Computer science made us think memories must always be loss-less, efficient, and organized like structured repositories. They can be split into standard-size slots, and every element can be stored in one or more slots. Once done, it’s enough to save two references: a pointer (a positional number, a couple of coordinates, or any other element) and the number of slots. For example, the book “War and Peace” (let’s suppose its length is 1000 units) can be stored in a memory at position 684, so the reference couple is (684, 1000). When necessary, it’s enough to retrieve 1000 units starting from position 684, and every single, exact word written by Tolstoj will appear in front of your eyes.
A RAM (Random Access Memory) works in this way (as well as Hard Disks and other similar supports). Is this an efficient storage strategy? Of course, it is, and every programmer knows how to work with this kind of memory. A variable has a type (which also determines its size). An array has a type and a dimensional structure. In both cases, it’s possible to access every element at a very high speed using names and indexes.
Now, let’s think about the small prey again. Is its memory structured in this way? Let’s suppose it is. The process can be described with the following steps: the sound is produced, and the pressure waves propagate at about 330 m/s and arrive at the ears. A complex mechanism transforms the sound into an electric signal sent to the brain, where a series of transformations should drive the recognition. If the memory were structured like a bookshelf, a scanning process should be performed, comparing each pattern with the new one. The most similar element has to be found as soon as possible, and the consequent action has to be chosen. The worst-case algorithm for a memory with n locations has this structure:
-
- For each memory location i:
- If Memory[i] == Element:
- return Element
- Else Continue
- If Memory[i] == Element:
- For each memory location i:
The computational cost is O(n), which is not so bad but requires a maximum number of n comparisons. A better solution is based on the concept of hash or signature (for further information, see Hash functions). Each element is associated with a (unique) hash, which can be an integer number used as an index for an over-complete array (N >> n). The computational cost for a good hash function is constant O(1), and so is the retrieval phase (because the hash is normally almost unique). However, another problem arises. A RAM-like memory needs exact locations or a complete scan, but instead of direct comparisons, it’s possible to use a similarity measure (that introduces some fuzziness, allowing to match noisy patterns). With a hash function, the computational cost is dramatically reduced, but the similarity becomes almost impossible because the algorithms are studied in order to generate completely different hashes, even for very small changes in the input.
At the end of the day, this kind of memory has too many problems, and a natural question is: how can animals manage them all? Indeed, animal brains avoid these problems completely. Their memory isn’t RAM, and all the information is stored completely differently. Without considering all the distinctions introduced by cognitive psychologists (short-term, long-term, work memory, and so on), we can say that an input pattern A, after some processing steps, is transformed into another pattern B:
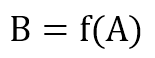
Normally, B has the same abilities as an original stimulus. This means that a correctly recognized roar elicits the same response as the sight of an actual lion, allowing a sort of prediction or action anticipation. Moreover, if A is partially corrupted with respect to the original version (here, we’re assuming Gaussian noise), the function is able to denoise its output:
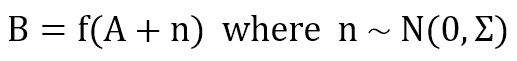
This approach is called associative, and it has been studied by several researchers (like [1] and [2]) in the fields of computer science and computational neurosciences. Many models (sometimes completely different in their mathematical formulation) have been designed and engineered (like BAMs, SOMs, and Hopfield Networks). However, their inner logic is always the same: a set of similar patterns (in terms of coarse-grained/fine-grained features) must elicit a similar response, and the inference time must be as short as possible. If you want to understand how some of these models work briefly, you can check these previous articles:
In order to summarize this idea, you can consider the following figure:
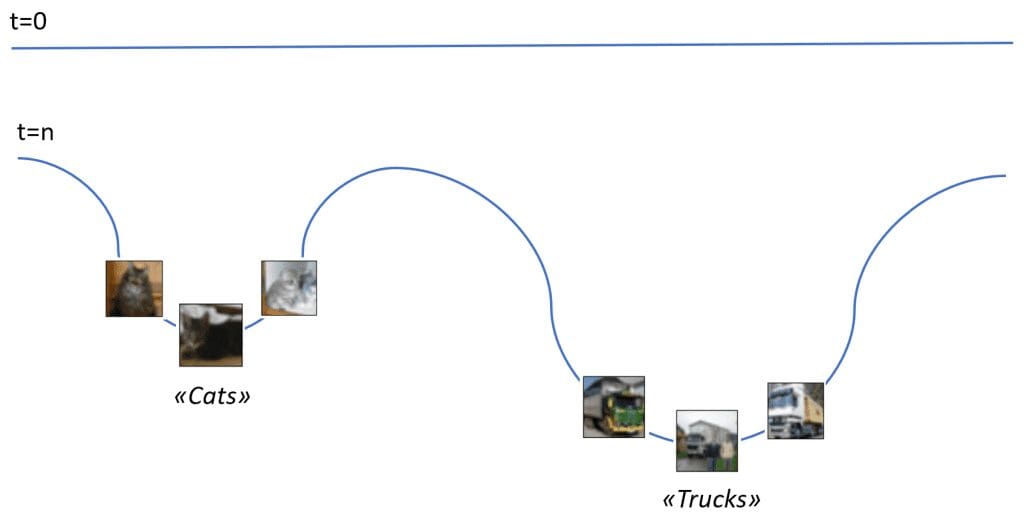
The blue line is the representation of a memory surface. At time t=0, nothing has been stored, and the line is straight. After some experience, two basins appear. With some fantasy, if the image of a new cat is sent close to the basin, it will fall down till reaching the minimum point, where the concept of “cat” is stored. The same happens for the category of “trucks” and so forth for any other semantic element associated with a specific perception. Even if this approach is based on the concept of energy and needs a dynamic evolution, it can be elegantly employed to explain the difference between random access and associate access. At the same time, retrieving a family of patterns and their common features is possible starting from a basin (which is a minimum in the memory surface). Immanuel Kant defined this as figurative synthesis and represents one of the most brilliant results the neocortex allows.
In fact, no specific images will be retrieved if somebody asks a person to think about a cat (assuming that this concept is not too familiar). On the contrary, a generic, feature-based representation is evoked and adapted to any possible instance belonging to the same family. To express this concept in a more concise way, we can say that we can recover whole concepts through the collection of common features and, if necessary, we can match these features with a real instance.
For example, some dogs are not very dissimilar to some cats, and it’s natural to ask: is it a dog or a cat? In this case, the set of features has a partial overlap, and we need to collect further pieces of information to reach a final decision. At the same time, if a cat is hidden behind a curtain and someone invites a friend to imagine it, all the possible features of the concept of “cat” will be recovered to allow guessing color, breed, and so on. Try yourself. Maybe the friend knows that fluffy animals are preferred, so he/she is driven to create the model in Persian. However, after a few seconds, a set of attributes is ready to be communicated.
Surprisingly, when the curtain is opened, a white bunny appears. In this case, the process is a bit more complex because the person trusted his/her friend and implicitly assigned a high priority to all pieces of information (also previously collected). Regarding probability, we say that the prior distribution peaked around the “cat” concept, avoiding spurious features that corrupt the mental model. (In the previous example, there were probably two smaller peaks around the concept of “cat” and “dog,” so the model could be partially noisy, allowing more freedom of choice).
When the image appears, almost none of the main predicted features match the bunny, driving the brain to reset its belief (not immediately because the prior keeps a minimum doubt). Luckily, this person has seen many rabbits before that moment, and even after all the wrong indications, his/her associative memories can rapidly recover a new concept, allowing the final decision that the animal isn’t a cat. A hard drive had to go back and forth many times, slowing down the process in a dramatic way.
A different approach based on Hetero-Encoders
A hetero-encoder is structurally identical to an auto-encoder. The only difference is the association: the latter trains a model in order to obtain:
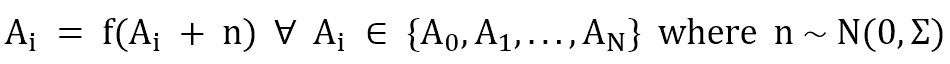
While a hetero-encoder trains a model that is able to perform the association:
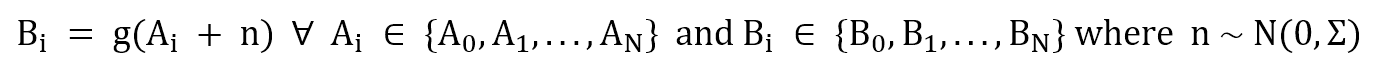
The source code is reported in this GIST and at the end of the article. It’s based on Tensorflow (Python 3.5) and split into an encoding part, a small convolutional network followed by a dense layer. It transforms the input (Batch size × 32 × 32 × 3) into a feature vector that can be fed into the decoder. This one processes the feature vector with a couple of dense layers and performs a deconvolution (transpose convolution) to build the output (Batch size × 32 × 32 × 3).
The model is trained using an L2 loss function computed on the difference between expected and predicted output. An extra L1 loss can be added to the feature vector to increase the sparsity. The training process takes a few minutes with GPU support and 500 epochs.
The model itself is not complex nor based on rocket science, but a few considerations are useful to understand why this approach is really important:
-
- The model is implicitly cumulative. In other words, the function g(•) works with all the input images, transforming them into the corresponding output.
- No, If statements are present. In the common algorithmic logic, g(•) should check for the input image and select the right transformation. On the contrary, a neural model can make this choice implicitly.
- All pattern transformations are stored in the parameter set whose plasticity allows continuous training.
- A noisy input version elicits a response with minimized L2 loss compared to the original one. Increasing the complexity of both the encoder and decoder makes it possible to increase the noise robustness further. This is a fundamental concept because having two identical perceptions is almost impossible.
In our “experiment,” the destination dataset is a shuffled version of the original one. Therefore, different periodic sequences are possible. I’m going to show this with some fictional fantasy. Each sequence has a fixed length of 20 pictures (19 associations). The first picture is freely chosen, while all the others are generated with a chain process.
Experience bricks
I’ve randomly selected (with fixed seed) 50 Cifar-10 pictures (through the Keras dataset loading function) as building blocks for the hetero-associative memory. Unfortunately, the categories are quite weird (frogs, ostriches, deer, cars, planes, trucks, and lovely cats), but they allow some fantasy to recreate the possible outline. The picture collage is shown in the following figure:

The original sequence (X_source) is then shuffled and turned into a destination sequence (X_dest). In this way, each original image will always be associated with another one belonging to the same group, and different periodic sequences can be discovered.
A few “stories”
The user can enlarge the dataset and experiment with different combinations. In this case, with 50 samples, I’ve discovered a few interesting sequences that I’ve called “stories.”
Period = 2

John was looking at a boat while a noisy truck behind him drew his attention to a concrete wall that was being built behind him.
Period = 7

While walking in a pet shop, John saw an exotic frog and suddenly remembered that he needed to buy food for his cat. His favorite brand is Acme Corp., and he has seen their truck several times. Meanwhile, the frog croaks, and he turns his head towards another terrarium. The color of the sand and the artificial landscape drive him to think about a ranch where he rode a horse for the first time. While trotting next to a pond, a duck drew his attention, and he was about to fall down. The frog croaked again at that moment, and he decided to hurry up.
Period = 7

John is looking at a small bird while remembering his grandpa, a passionate bird-watcher. He had an old light-blue car, and when John was a child, he saw an ostrich during a short trip with his grandpa. Their small dog began barking, and he asked his grandpa to speed up, but he answered: “Hey, this is not a Ferrari!” (Ok, my fantasy is going too fast…). During the same trip, they saw a deer, and John took a photo with his brand-new camera.
Period = 20 (two stories partially overlapped)
Story A:

Story B:

These two cases are slightly more complex, and I prefer not to fantasize. The concept is always the same: an input drives the network to produce an association B (which can be made up of visual, auditory, olfactory, … elements). B can elicit a new response C and so on.
Two elements are interesting, and they are worth an investigation:
-
- Using a Recurrent Neural Network (like an LSTM) to process short sequences with different components (like pictures and sounds)
- Adding a “subconscious” layer that can influence the output according to a partially autonomous process.
Source code
import matplotlib.pyplot as plt
import multiprocessing
import numpy as np
import tensorflow as tf
from keras.datasets import cifar10
# Set random seed (for reproducibility)
np.random.seed(1000)
tf.set_random_seed(1000)
width = 32
height = 32
batch_size = 10
nb_epochs = 500
code_length = 1024
use_gpu = True
# Load the dataset
(X_train, Y_train), (X_test, Y_test) = cifar10.load_data()
# Select 50 samples
X_source = X_train[0:50]
X_dest = X_source.copy()
np.random.shuffle(X_dest)
def encoder(encoder_input):
# Convolutional layer 1
conv1 = tf.layers.conv2d(inputs=encoder_input,
filters=32,
kernel_size=(3, 3),
kernel_initializer=tf.contrib.layers.xavier_initializer(),
activation=tf.nn.tanh)
# Convolutional output (flattened)
conv_output = tf.contrib.layers.flatten(conv1)
# Encoder Dense layer 1
d_layer_1 = tf.layers.dense(inputs=conv_output,
units=1024,
activation=tf.nn.tanh)
# Code layer
code_layer = tf.layers.dense(inputs=d_layer_1,
units=code_length,
activation=tf.nn.tanh)
return code_layer
def decoder(code_sequence, bs):
# Decoder Dense layer 1
d_layer_1 = tf.layers.dense(inputs=code_sequence,
units=1024,
activation=tf.nn.tanh)
# Code output layer
code_output = tf.layers.dense(inputs=d_layer_1,
units=(height - 2) * (width - 2) * 3,
activation=tf.nn.tanh)
# Deconvolution input
deconv_input = tf.reshape(code_output, (bs, height - 2, width - 2, 3))
# Deconvolution layer 1
deconv1 = tf.layers.conv2d_transpose(inputs=deconv_input,
filters=3,
kernel_size=(3, 3),
kernel_initializer=tf.contrib.layers.xavier_initializer(),
activation=tf.sigmoid)
# Output batch
output_batch = tf.cast(tf.reshape(deconv1, (bs, height, width, 3)) * 255.0, tf.uint8)
return deconv1, output_batch
def create_batch(t):
X = np.zeros((batch_size, height, width, 3), dtype=np.float32)
Y = np.zeros((batch_size, height, width, 3), dtype=np.float32)
if t < X_source.shape[0] - batch_size:
tmax = t + batch_size
else:
tmax = X_source.shape[0]
for k, image in enumerate(X_source[t:tmax]):
X[k, :, :, :] = image / 255.0
for k, image in enumerate(X_dest[t:tmax]):
Y[k, :, :, :] = image / 255.0
return X, Y
# Create a Tensorflow Graph
graph = tf.Graph()
with graph.as_default():
with tf.device('/cpu:0'):
# Global step
global_step = tf.Variable(0, trainable=False)
with tf.device('/gpu:0' if use_gpu else '/cpu:0'):
# Input batch
input_images = tf.placeholder(tf.float32, shape=(None, height, width, 3))
# Output batch
output_images = tf.placeholder(tf.float32, shape=(None, height, width, 3))
# Batch_size
t_batch_size = tf.placeholder(tf.int32, shape=())
# Encoder
code_layer = encoder(encoder_input=input_images)
# Decoder
deconv_output, output_batch = decoder(code_sequence=code_layer,
bs=t_batch_size)
# Reconstruction L2 loss
loss = tf.nn.l2_loss(output_images - deconv_output)
# Training operations
learning_rate = tf.train.exponential_decay(learning_rate=0.00025,
global_step=global_step,
decay_steps=int(X_source.shape[0] / (2 * batch_size)),
decay_rate=0.9,
staircase=True)
trainer = tf.train.AdamOptimizer(learning_rate=learning_rate)
training_step = trainer.minimize(loss)
def predict(X, bs=1):
feed_dict = {
input_images: X.reshape((1, height, width, 3)) / 255.0,
output_images: np.zeros((bs, height, width, 3), dtype=np.float32),
t_batch_size: bs
}
return session.run([output_batch], feed_dict=feed_dict)[0]
def story(t):
oimages = np.zeros(shape=(20, height, width, 3), dtype=np.uint8)
oimages[0, :, :, :] = X_source[t]
for i in range(1, 20):
oimages[i, :, :, :] = predict(oimages[i - 1])
fig, ax = plt.subplots(2, 10, figsize=(18, 4))
for i in range(2):
for j in range(10):
ax[i, j].get_xaxis().set_visible(False)
ax[i, j].get_yaxis().set_visible(False)
ax[i, j].imshow(oimages[(10 * i) + j])
plt.show()
if __name__ == '__main__':
# Create a Tensorflow Session
config = tf.ConfigProto(intra_op_parallelism_threads=multiprocessing.cpu_count(),
inter_op_parallelism_threads=multiprocessing.cpu_count(),
allow_soft_placement=True,
device_count={'CPU': 1,
'GPU': 1 if use_gpu else 0})
session = tf.InteractiveSession(graph=graph, config=config)
# Initialize all variables
tf.global_variables_initializer().run()
# Train the model
for e in range(nb_epochs):
total_loss = 0.0
for t in range(0, X_source.shape[0], batch_size):
X, Y = create_batch(t)
feed_dict = {
input_images: X,
output_images: Y,
t_batch_size: batch_size
}
_, t_loss = session.run([training_step, loss], feed_dict=feed_dict)
total_loss += t_loss
print('Epoch {} - Loss: {}'.
format(e + 1,
total_loss / float(X_train.shape[0])))
# Show some stories
story(0)
# story(1)
# story(9)
# ...
References
-
- Kosko B., Bidirectional Associative Memory, IEEE Transactions on Systems, Man, and Cybernetics, v. 18/1, 1988
- Dayan P., Abbott L. F., Theoretical Neuroscience, The MIT Press
- Trappenberg T., Fundamentals of Computational Neuroscience, Oxford University Press
- Izhikevich E. M., Dynamical Systems in Neuroscience, The MIT Press
- Rieke F., Warland D., Ruyter Van Steveninck R., Bialek W., Spikes: Exploring the Neural Code, A Bradford Book
If you like this post, you can always donate to support my activity! One coffee is enough!

