Hopfield networks (named after the scientist John Hopfield) are a family of recurrent neural networks with bipolar thresholded neurons. Even if more efficient models replace them, they represent an excellent example of associative memory based on shaping an energy surface. In the following picture, there’s the generic schema of a Hopfield network with three neurons:
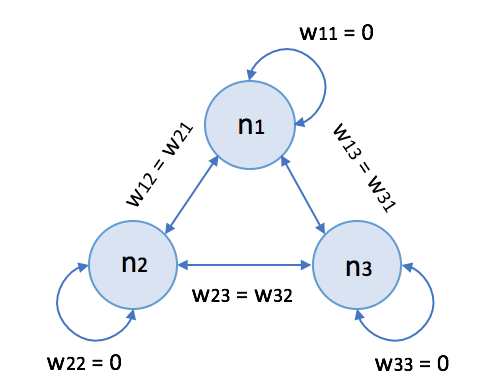
Conventionally, the synaptic weights obey the following conditions:
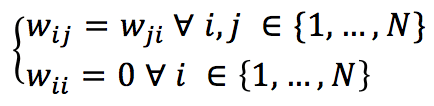
If we have N neurons, the generic input vector must be N-dimension and bipolar (-1 and 1 values). The activation function for each neuron is hence defined as:
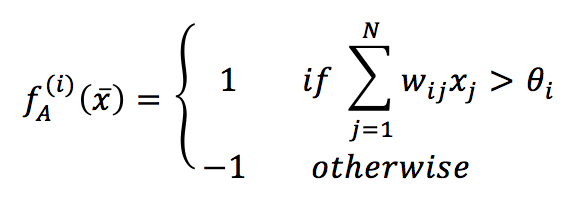
In the previous formula, the threshold for each neuron is represented by θ (a common value is 0, which implies a strong symmetry). Contrary to MLP, this kind of network does not separate input and output layers. Each unit can receive its input value, process it, and output the result. According to the original theory, it’s possible to update the network in two ways:
-
- Synchronous: all units compute their activation at the same time
- Asynchronous: the units compute the activations following a fixed or random sequence
The first approach is less biologically plausible, and most efforts are focused on the second strategy. At this point, it’s useful to introduce another concept that is peculiar to this kind of network: an energy function. We can define the energy of a Hopfield network as:
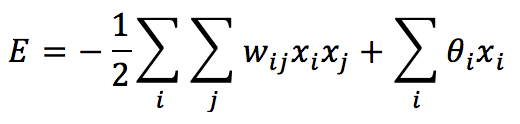
If the weights are null and no input is applied, E = 0 is the initial condition for every network. However, we need to employ this model as associative memory. Therefore, our task is to “reshape” the energy surface so as to store the patterns (attractors) in the local minima of E:
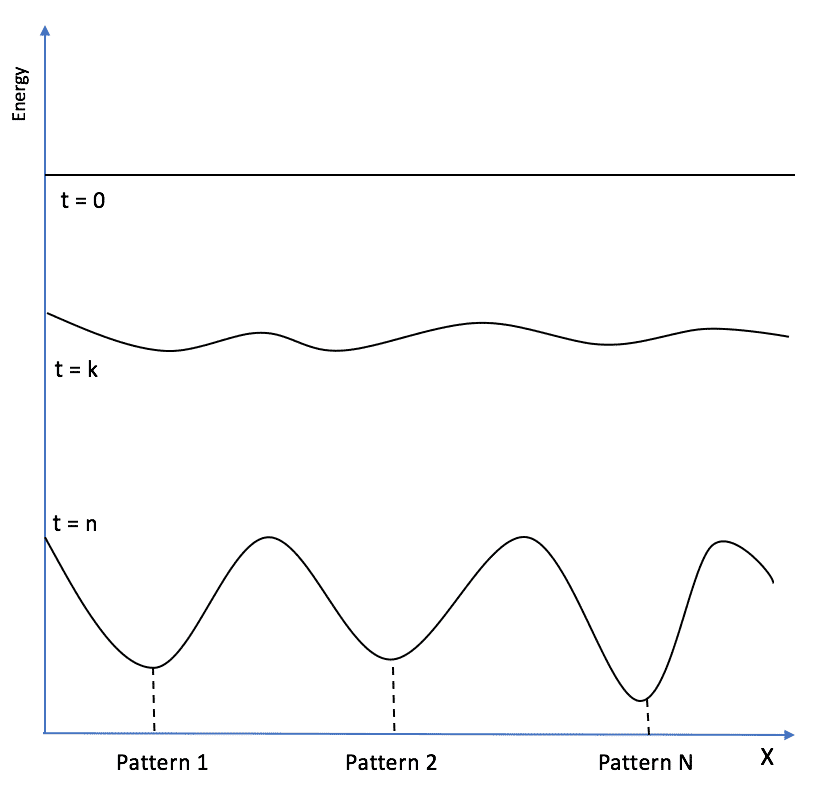
To determine the optimal learning rule, we need to consider that a new pattern has to reduce the total energy, finding an existing or a new local minimum that can represent its structure. Let’s consider a network that has already stored M patterns. We can rewrite the energy (for simplicity, we can set all thresholds to zero) to separate the “old” part from the one due to the new pattern:
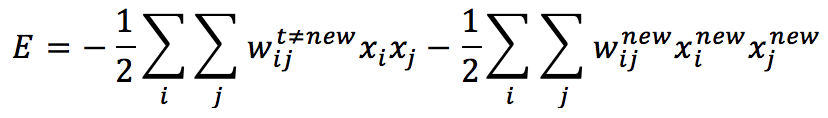
In order to reduce global energy consumption, we need to increase the absolute value of the second term, it’s easy to understand that choosing:
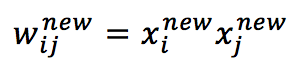
The second term becomes:
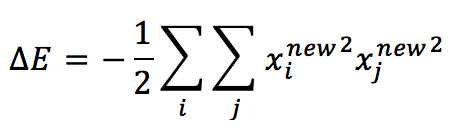
Which is always non-positive and contributes to reducing the total energy. This conclusion allows us to define the learning rule for a Hopfield network (which is actually an extended Hebbian rule):
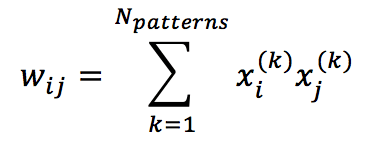
One of the worst drawbacks of Hopfield networks is the capacity. In fact, Hertz, Krogh, and Palmer (in Introduction to Theory of Neural Computation) have proven that a bipolar network with N>>1 neurons can permanently store max 0.138N patterns (about 14%) with an error probability less than 0.36%. This means, for example, that we have at least 138 neurons to store the digits 0 to 9.
Let’s see a simple example written in Python (the code can be vectorized in order to improve the performances) with four basic 4×4 patterns:

The code is available on this GIST:
import matplotlib.pyplot as plt
import numpy as np
# Set random seed for reproducibility
np.random.seed(1000)
nb_patterns = 4
pattern_width = 4
pattern_height = 4
max_iterations = 10
# Initialize the patterns
X = np.zeros((nb_patterns, pattern_width * pattern_height))
X[0] = [-1, 1, 1, -1, -1, 1, 1, -1, -1, 1, 1, -1, -1, 1, 1, -1]
X[1] = [-1, -1, -1, -1, 1, 1, 1, 1, 1, 1, 1, 1, -1, -1, -1, -1]
X[2] = [-1, -1, 1, 1, -1, -1, 1, 1, 1, 1, -1, -1, 1, 1, -1, -1]
X[3] = [1, 1, -1, -1, 1, 1, -1, -1, -1, -1, 1, 1, -1, -1, 1, 1]
# Show the patterns
fig, ax = plt.subplots(1, nb_patterns, figsize=(10, 5))
for i in range(nb_patterns):
ax[i].matshow(X[i].reshape((pattern_height, pattern_width)), cmap='gray')
ax[i].set_xticks([])
ax[i].set_yticks([])
plt.show()
# Train the network
W = np.zeros((pattern_width * pattern_height, pattern_width * pattern_height))
for i in range(pattern_width * pattern_height):
for j in range(pattern_width * pattern_height):
if i == j or W[i, j] != 0.0:
continue
w = 0.0
for n in range(nb_patterns):
w += X[n, i] * X[n, j]
W[i, j] = w / X.shape[0]
W[j, i] = W[i, j]
# Create a corrupted test pattern
x_test = np.array([1, -1, 1, 1, -1, -1, 1, 1, -1, 1, -1, -1, 1, 1, 1, 1])
# Recover the original patterns
A = x_test.copy()
for _ in range(max_iterations):
for i in range(pattern_width * pattern_height):
A[i] = 1.0 if np.dot(W[i], A) > 0 else -1.0
# Show corrupted and recovered patterns
fig, ax = plt.subplots(1, 2, figsize=(10, 5))
ax[0].matshow(x_test.reshape(pattern_height, pattern_width), cmap='gray')
ax[0].set_title('Corrupted pattern')
ax[0].set_xticks([])
ax[0].set_yticks([])
ax[1].matshow(A.reshape(pattern_height, pattern_width), cmap='gray')
ax[1].set_title('Recovered pattern')
ax[1].set_xticks([])
ax[1].set_yticks([])
plt.show()
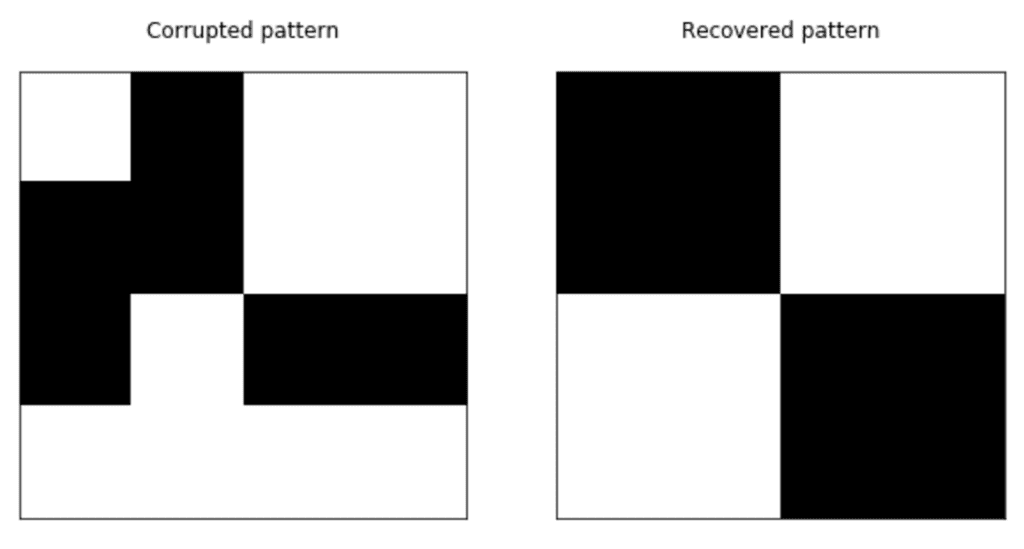
We have trained the network and proposed a corrupted pattern that has been attracted by the nearest energy local minimum where the original version has been stored:
Implementing a stochastic process based on a probability distribution obtained using the sigmoid function is also possible. In this case, each neuron (the threshold is set to null) is activated according to the probability:
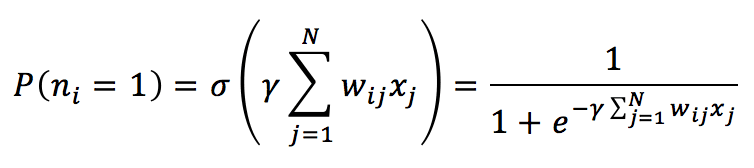
The parameter ϒ is related to the Boltzmann distribution and is generally considered as the reciprocal of the absolute temperature. If T >> 1, ϒ is close to 0, the P is about 0.5. When T decreases, ϒ increases, and P approaches to value 1. For our purposes, it’s possible to set it to 1. The process is very similar to the one already explained, with the difference that the activation of a neuron is random. Once P(n=1) has been computed, it’s possible to sample a value from a uniform distribution (for example, between 0 and 1) and check whether the value is less than P(n=1). If it is, the neuron is activated (state = 1); otherwise, its state is set to -1. The process must be iterated a fixed number of times or until the pattern becomes stable.
For any further information, I suggest:
-
- Hertz J.A, Krogh A.S., Palmer R.G, Introduction To The Theory Of Neural Computation, Santa Fe Institute Series
If you like this post, you can always donate to support my activity! One coffee is enough!

