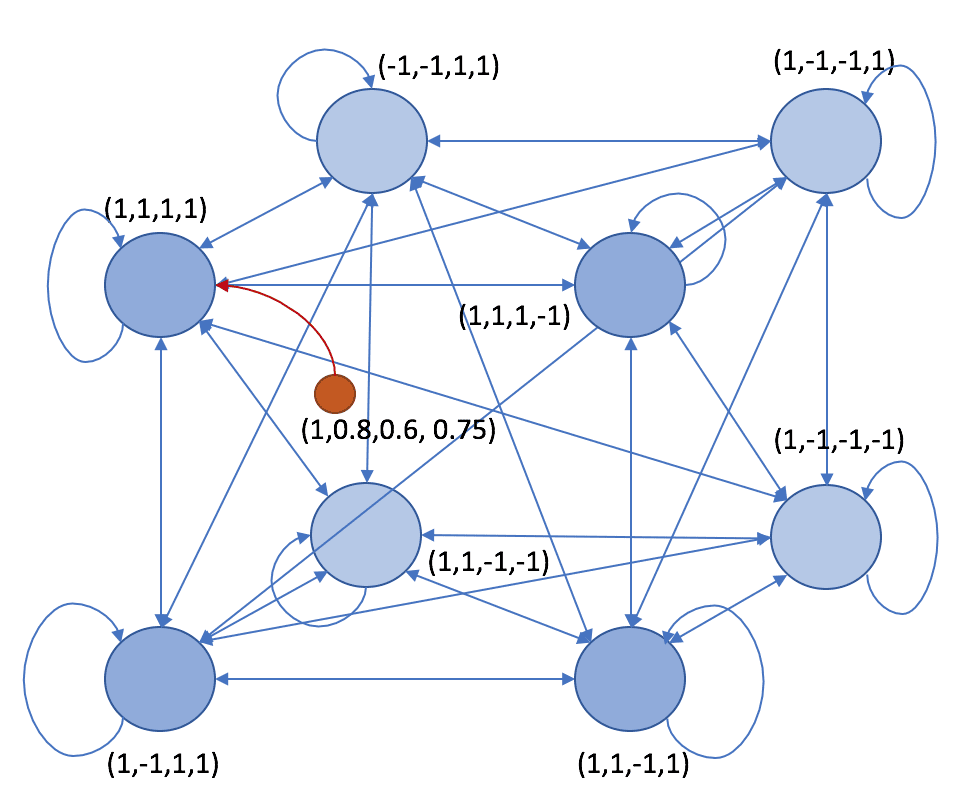
The Brain-State-in-a-Box is a neural model proposed by Anderson, Silverstein, Ritz, and Jones in 1977 that presents very strong analogies with Hopfield networks (read the previous post about them). The network structure is similar: recurrent, fully connected with symmetric weights and non-null auto-recurrent connections. All neurons are bipolar (-1 and 1). If there are N neurons, it’s possible to imagine an N-dimensional hypercube:
The main difference with a Hopfield network is the activation function:
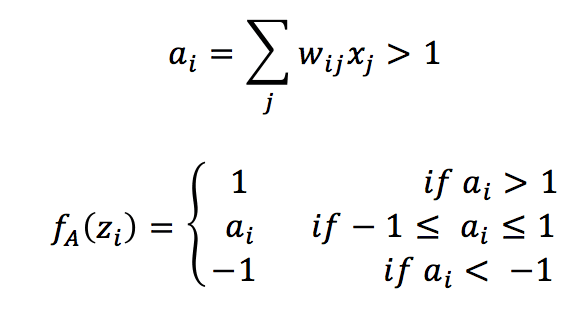
And the dynamics that, in this case, is synchronous. Therefore, all neurons are updated at the same time.
The activation function is linear when the weighted input a(i) is bounded between -1 and 1 and saturates to -1 and 1 outside the boundaries. A stable state of the network is one of the hypercube vertices (that’s why it’s called in this way). The training rule is always an extended Hebbian based on the pre-synaptic and post-synaptic raw input:
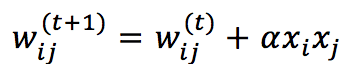
Where α is the learning rate.
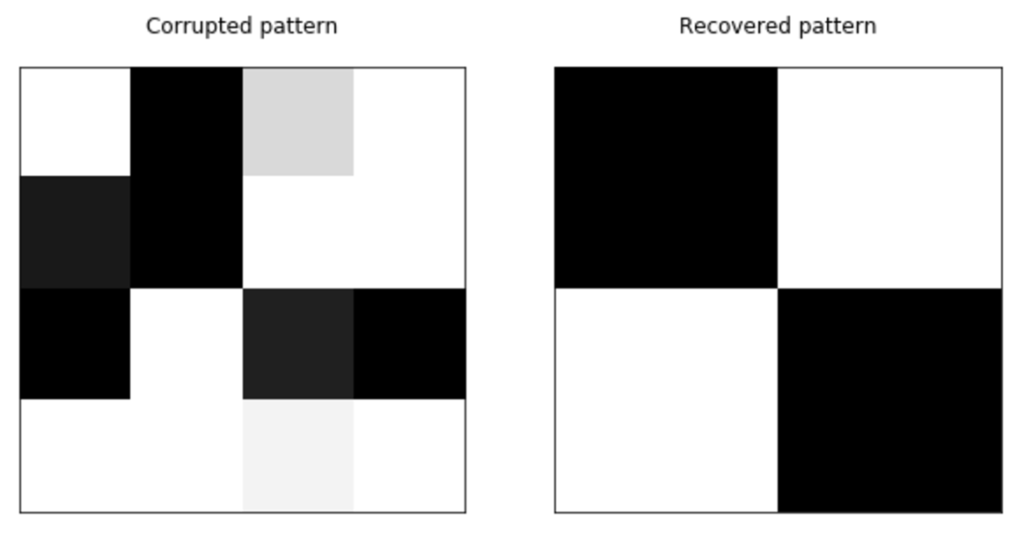
The learning procedure is analogous to the one employed for Hopfield Networks (iteration of the weight updates until convergence), while the recovery of a pattern starting from a corrupted one is now “filtered” by the saturated activation function. When a noisy pattern is presented, all the activations are computed, and the procedure is repeated until the network converges to a stable state.
The example is based on the Hopfield networks one, and it’s available on this GIST:
import matplotlib.pyplot as plt
import numpy as np
# Set random seed for reproducibility
np.random.seed(1000)
nb_patterns = 4
pattern_width = 4
pattern_height = 4
max_iterations = 100
learning_rate = 0.5
# Initialize the patterns
X = np.zeros((nb_patterns, pattern_width * pattern_height))
X[0] = [-1, 1, 1, -1, -1, 1, 1, -1, -1, 1, 1, -1, -1, 1, 1, -1]
X[1] = [-1, -1, -1, -1, 1, 1, 1, 1, 1, 1, 1, 1, -1, -1, -1, -1]
X[2] = [-1, -1, 1, 1, -1, -1, 1, 1, 1, 1, -1, -1, 1, 1, -1, -1]
X[3] = [1, 1, -1, -1, 1, 1, -1, -1, -1, -1, 1, 1, -1, -1, 1, 1]
# Show the patterns
fig, ax = plt.subplots(1, nb_patterns, figsize=(10, 5))
for i in range(nb_patterns):
ax[i].matshow(X[i].reshape((pattern_height, pattern_width)), cmap='gray')
ax[i].set_xticks([])
ax[i].set_yticks([])
plt.show()
# Initialize the weight matrix
W = np.random.uniform(-0.1, 0.1, size=(pattern_width * pattern_height, pattern_width * pattern_height))
W = W + W.T
# Create a vectorized activation function
def activation(x):
if x > 1.0:
return 1.0
elif x < -1.0:
return -1.0
else:
return x
act = np.vectorize(activation)
# Train the network
for _ in range(max_iterations):
for n in range(nb_patterns):
for i in range(pattern_width * pattern_height):
for j in range(pattern_width * pattern_height):
W[i, j] += learning_rate * X[n, i] * X[n, j]
W[j, i] = W[i, j]
# Create a corrupted test pattern
x_test = np.array([1, -1, 0.7, 1, -0.8, -1, 1, 1, -1, 1, -0.75, -1, 1, 1, 0.9, 1])
# Recover the original patterns
A = x_test.copy()
for _ in range(max_iterations):
for i in range(pattern_width * pattern_height):
A[i] = activation(np.dot(W[i], A))
# Show corrupted and recovered patterns
fig, ax = plt.subplots(1, 2, figsize=(10, 5))
ax[0].matshow(x_test.reshape(pattern_height, pattern_width), cmap='gray')
ax[0].set_title('Corrupted pattern')
ax[0].set_xticks([])
ax[0].set_yticks([])
ax[1].matshow(A.reshape(pattern_height, pattern_width), cmap='gray')
ax[1].set_title('Recovered pattern')
ax[1].set_xticks([])
ax[1].set_yticks([])
plt.show()
However, in this case, we have created a pattern that is “inside” the box because some of the values are between -1 and 1:
For any further information, I suggest:
-
- Hertz J.A, Krogh A.S., Palmer R.G, Introduction To The Theory Of Neural Computation, Santa Fe Institute Series
If you like this post, you can always donate to support my activity! One coffee is enough!

