Le reti di Hopfield (dal nome dello scienziato John Hopfield) sono una famiglia di reti neurali ricorrenti con neuroni bipolari a soglia. Anche se modelli più efficienti li sostituiscono, rappresentano un ottimo esempio di memoria associativa basata sulla modellazione di una superficie energetica. Nell’immagine seguente, c’è lo schema generico di una rete di Hopfield con tre neuroni:
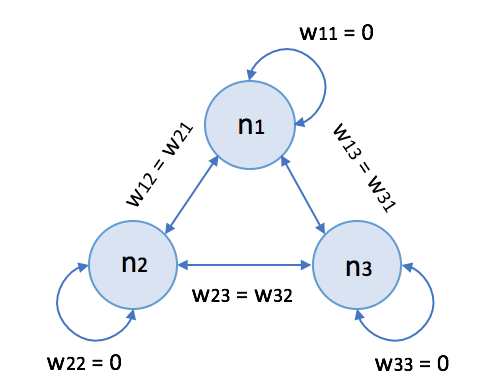
Convenzionalmente, i pesi sinaptici obbediscono alle seguenti condizioni:
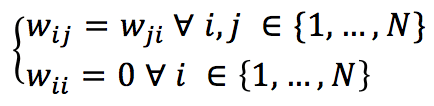
Se abbiamo N neuroni, il vettore di ingresso generico deve essere di dimensione N e bipolare (valori -1 e 1). La funzione di attivazione per ogni neurone è quindi definita come:
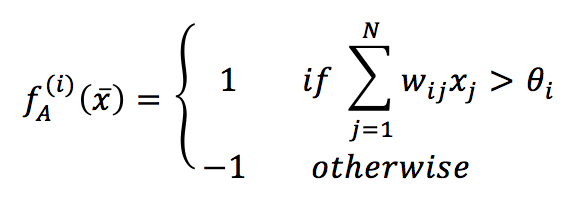
Nella formula precedente, la soglia per ogni neurone è rappresentata da θ (un valore comune è 0, che implica una forte simmetria). A differenza di MLP, questo tipo di rete non separa gli strati di ingresso e di uscita. Ogni unità può ricevere il suo valore di ingresso, elaborarlo e produrre il risultato. Secondo la teoria originale, è possibile aggiornare la rete in due modi:
-
- Sincrono: tutte le unità calcolano la loro attivazione nello stesso momento.
- Asincrono: le unità calcolano le attivazioni seguendo una sequenza fissa o casuale.
Il primo approccio è meno plausibile dal punto di vista biologico e la maggior parte degli sforzi si concentra sulla seconda strategia. A questo punto, è utile introdurre un altro concetto che è peculiare di questo tipo di rete: una funzione energetica. Possiamo definire l’energia di una rete di Hopfield come:
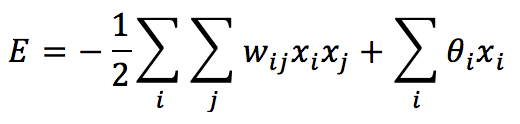
Se i pesi sono nulli e non viene applicato alcun input, E = 0 è la condizione iniziale di ogni rete. Tuttavia, dobbiamo impiegare questo modello come memoria associativa. Pertanto, il nostro compito è quello di ‘rimodellare’ la superficie energetica in modo da memorizzare i modelli (attrattori) nei minimi locali di E:
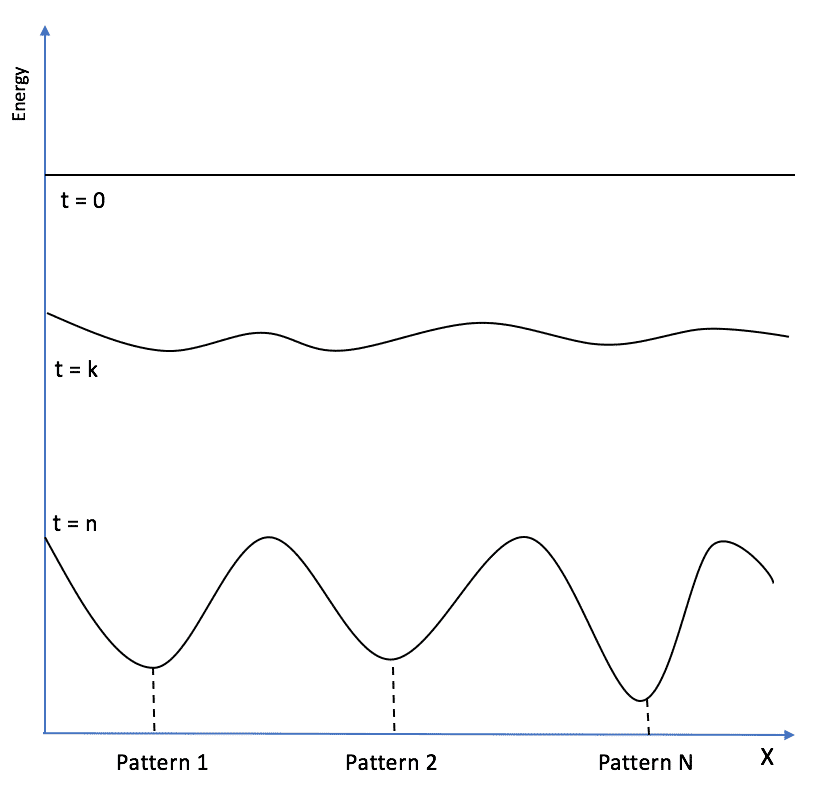
Per determinare la regola di apprendimento ottimale, dobbiamo considerare che un nuovo modello deve ridurre l’energia totale, trovando un minimo locale esistente o nuovo che possa rappresentare la sua struttura. Consideriamo una rete che ha già memorizzato M modelli. Possiamo riscrivere l’energia (per semplicità, possiamo impostare tutte le soglie a zero) per separare la parte “vecchia” da quella dovuta al nuovo modello:
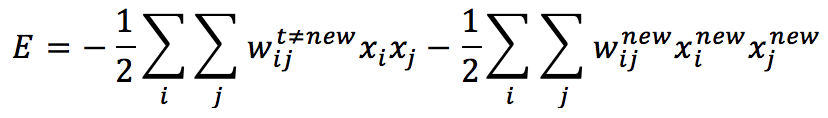
Per ridurre il consumo energetico globale, dobbiamo aumentare il valore assoluto del secondo termine, è facile capire che scegliere:
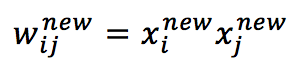
Il secondo termine diventa:
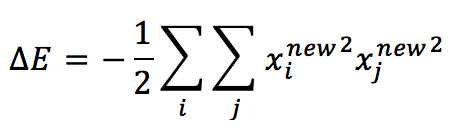
Che è sempre non positivo e contribuisce a ridurre l’energia totale. Questa conclusione ci permette di definire la regola di apprendimento per una rete di Hopfield (che in realtà è una regola Hebbiana estesa):
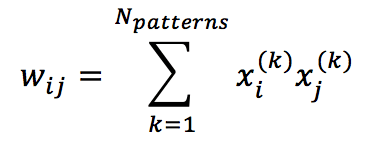
Uno dei peggiori inconvenienti delle reti di Hopfield è la capacità. Infatti, Hertz, Krogh e Palmer (in Introduction to Theory of Neural Computation) hanno dimostrato che una rete bipolare con N>>1 neuroni possono memorizzare in modo permanente un massimo di 0,138N modelli (circa il 14%) con una probabilità di errore inferiore allo 0,36%. Ciò significa, ad esempio, che abbiamo almeno 138 neuroni per memorizzare le cifre da 0 a 9.
Vediamo un semplice esempio scritto in Python (il codice può essere vettorializzato per migliorare le prestazioni) con quattro modelli 4×4 di base:

Il codice è disponibile su questo GIST:
import matplotlib.pyplot as plt
import numpy as np
# Set random seed for reproducibility
np.random.seed(1000)
nb_patterns = 4
pattern_width = 4
pattern_height = 4
max_iterations = 10
# Initialize the patterns
X = np.zeros((nb_patterns, pattern_width * pattern_height))
X[0] = [-1, 1, 1, -1, -1, 1, 1, -1, -1, 1, 1, -1, -1, 1, 1, -1]
X[1] = [-1, -1, -1, -1, 1, 1, 1, 1, 1, 1, 1, 1, -1, -1, -1, -1]
X[2] = [-1, -1, 1, 1, -1, -1, 1, 1, 1, 1, -1, -1, 1, 1, -1, -1]
X[3] = [1, 1, -1, -1, 1, 1, -1, -1, -1, -1, 1, 1, -1, -1, 1, 1]
# Show the patterns
fig, ax = plt.subplots(1, nb_patterns, figsize=(10, 5))
for i in range(nb_patterns):
ax[i].matshow(X[i].reshape((pattern_height, pattern_width)), cmap='gray')
ax[i].set_xticks([])
ax[i].set_yticks([])
plt.show()
# Train the network
W = np.zeros((pattern_width * pattern_height, pattern_width * pattern_height))
for i in range(pattern_width * pattern_height):
for j in range(pattern_width * pattern_height):
if i == j or W[i, j] != 0.0:
continue
w = 0.0
for n in range(nb_patterns):
w += X[n, i] * X[n, j]
W[i, j] = w / X.shape[0]
W[j, i] = W[i, j]
# Create a corrupted test pattern
x_test = np.array([1, -1, 1, 1, -1, -1, 1, 1, -1, 1, -1, -1, 1, 1, 1, 1])
# Recover the original patterns
A = x_test.copy()
for _ in range(max_iterations):
for i in range(pattern_width * pattern_height):
A[i] = 1.0 if np.dot(W[i], A) > 0 else -1.0
# Show corrupted and recovered patterns
fig, ax = plt.subplots(1, 2, figsize=(10, 5))
ax[0].matshow(x_test.reshape(pattern_height, pattern_width), cmap='gray')
ax[0].set_title('Corrupted pattern')
ax[0].set_xticks([])
ax[0].set_yticks([])
ax[1].matshow(A.reshape(pattern_height, pattern_width), cmap='gray')
ax[1].set_title('Recovered pattern')
ax[1].set_xticks([])
ax[1].set_yticks([])
plt.show()
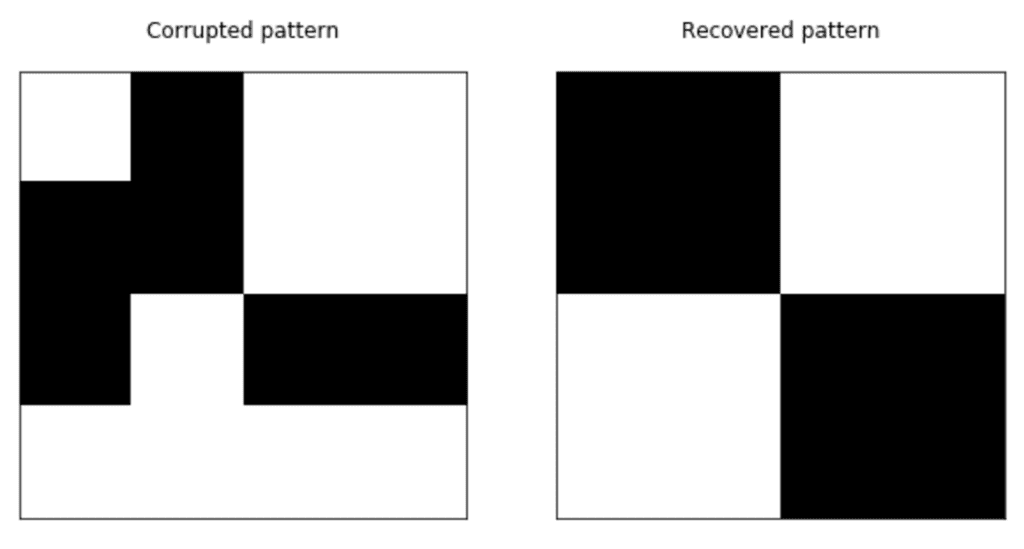
Abbiamo addestrato la rete e proposto un modello corrotto che è stato attratto dal minimo locale energetico più vicino, dove è stata memorizzata la versione originale:
È possibile anche implementare un processo stocastico basato su una distribuzione di probabilità ottenuta con la funzione sigmoide. In questo caso, ogni neurone (la soglia è impostata su nullo) viene attivato in base alla probabilità:
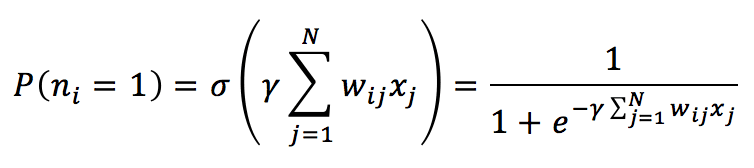
Il parametro ϒ è legato alla distribuzione di Boltzmann e viene normalmente considerato come il reciproco della temperatura assoluta. Se T >> 1, ϒ è vicino a 0, la P è di circa 0,5. Quando T diminuisce, ϒ aumenta, e P si avvicina al valore 1. Per i nostri scopi, è possibile impostarla su 1. Il processo è molto simile a quello già spiegato, con la differenza che l’attivazione di un neurone è casuale. Una volta calcolato P(n=1), è possibile campionare un valore da una distribuzione uniforme (ad esempio, tra 0 e 1) e verificare se il valore è inferiore a P(n=1). Se lo è, il neurone viene attivato (stato = 1); altrimenti, il suo stato viene impostato su -1. Il processo deve essere iterato per un numero fisso di volte o fino a quando il modello diventa stabile.
Per ulteriori informazioni, le suggerisco:
-
- Hertz J.A, Krogh A.S., Palmer R.G, Introduction To The Theory Of Neural Computation, Santa Fe Institute Series
Se ti piace l’articolo, puoi sempre fare una donazione per supportare la mia attività. Basta un caffè!

