The Hodgkin-Huxley model (published in 1952 in The Journal of Physiology [1]) is the most famous spiking neuron model (also if there are simpler alternatives like the “Integrate-and-fire” model, which performs exceptionally well).
It comprises a system of four ordinary differential equations that can be easily integrated using several different tools. The main idea is based on an electrical representation of the neuron, considering only Potassium (K) and Sodium (Na) voltage-gated ion channels (even if they can be extended to include more channels). A schematic representation is shown in the following figure:
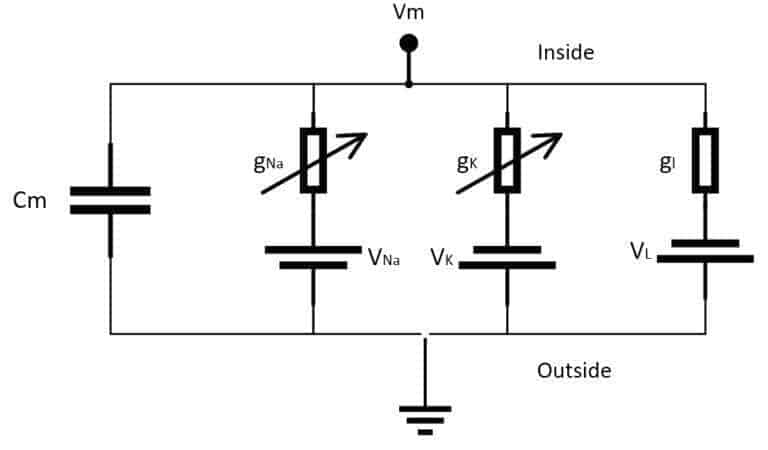
The elements are:
-
- Cm: a capacitance per unit area representing the membrane lipid-bilayer (adopted value: 1 µF/cm²)
- gNa: voltage-controlled conductance per unit area associated with the Sodium (Na) ion channel (adopted value: 120 µS/cm²)
- gK: voltage-controlled conductance per unit area associated with the Potassium (K) ion channel (adopted value: 36 µS/cm²)
- gl: conductance per unit area associated with the leak channels (adopted value: 0.3 36 µS/cm²)
- VNa: voltage source representing the electrochemical gradient for Sodium ions (adopted value: 115 mV)
- VK: voltage source representing the electrochemical gradient for Potassium ions (adopted value: -12 mV)
- Vl: voltage source that determines the leakage current density together with gl (adopted value: 10.613 mV)
In the scheme, the external stimulus current is not shown. However, we assume its presence as a current density (I) encoding the input signal. All the experimental values are the same as proposed by the authors in [1] and refer to an equilibrium potential of 0 V. The system is defined through the following ODE system:
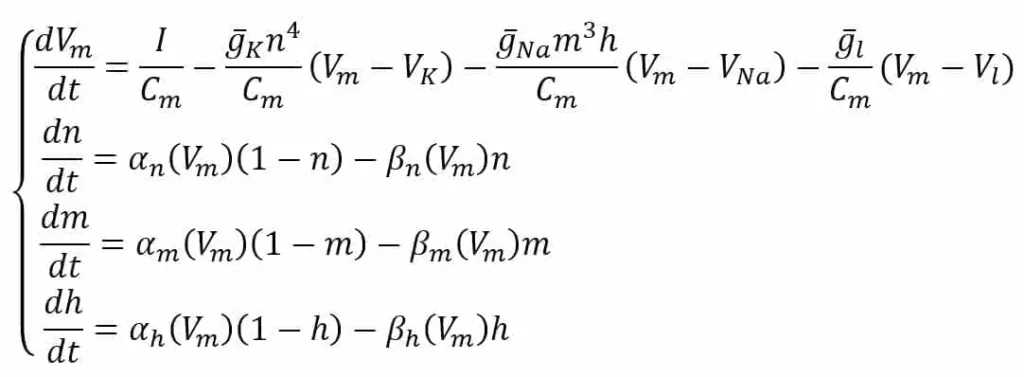
The first equation defines the derivative of Vm considering the external stimulus (I) and the contribution of K, Na, and leakage current densities. The variables n, m, and h are associated with the probability of each channel to open and strictly depend on the nature of the channel. For example, the K channel is voltage-gated and has four sub-units that must all be open to allow the current to flow; therefore, its probability is n to the power of 4.
Sodium has a slightly more complex behavior and needs two factors (m and h) with autonomous dynamics. The last three equations describe the ion-channel kinetic model by computing the derivatives of n, m, and h as functions of the same variables and two voltage-dependent functions. The first term is the number of closed channels opening, while the second term is the number of open channels closing.
Hodgkin and Huxley suggest the following functions:
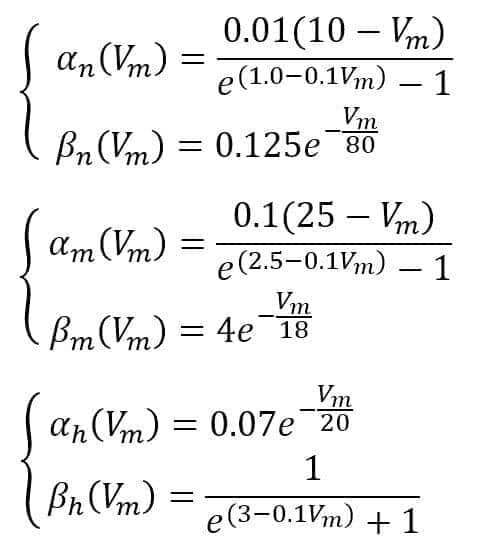
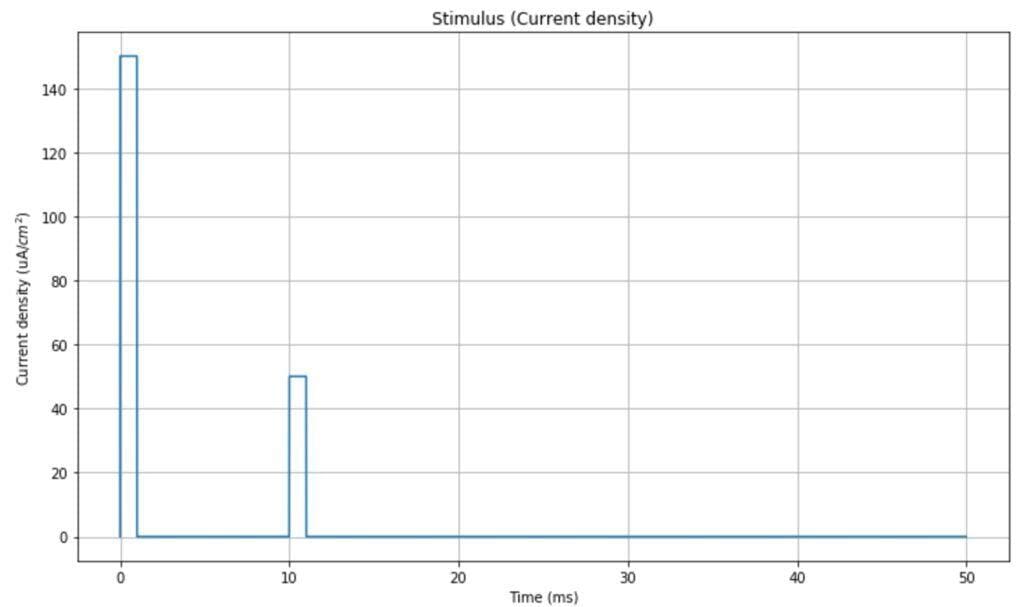
In the simulation, we will use a double-impulsive current density as a stimulus (however, any other signal can be used to test different behaviors). The time range is [0, 50ms]:
The resulting impulsive neuron behavior is shown in the following plot:
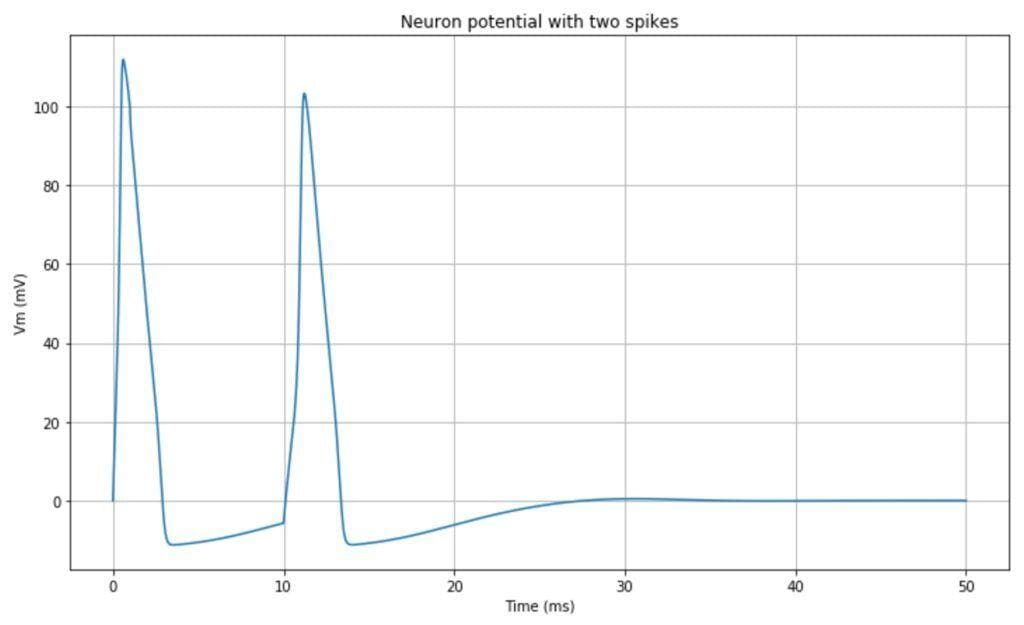
It’s also possible to observe the limit cycles present in the dynamic system. In the following plot, the trajectories Vm – n, and Vm – m are plotted:
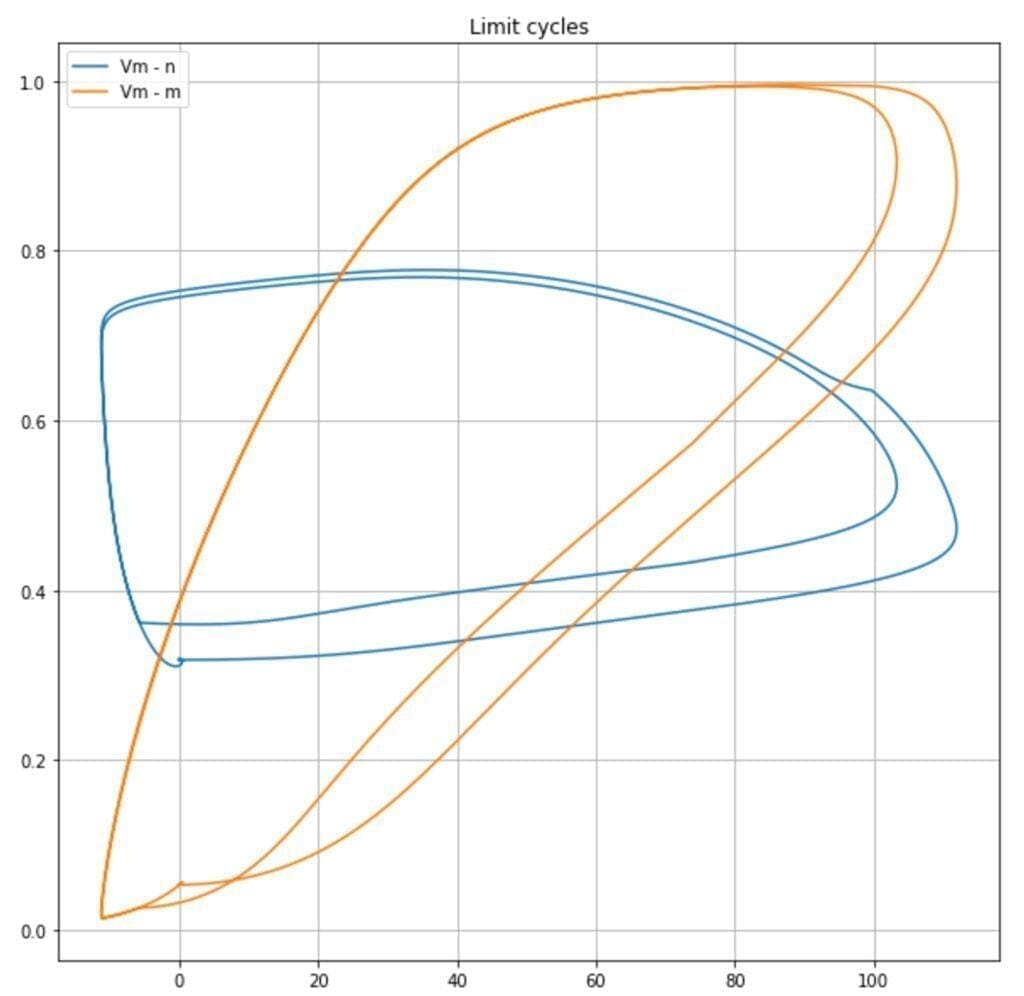
It’s possible to observe how the probabilities (proportional to n, m, and h) for ion channels to be opened span from a minimum to a maximum value according to n and Vm in a cyclic fashion. This allows the oscillations: steady state, potential increase, spike, potential decrease, steady state.
The complete Python code is available in this GIST:
import matplotlib.pyplot as plt
import numpy as np
from scipy.integrate import odeint
# Set random seed (for reproducibility)
np.random.seed(1000)
# Start and end time (in milliseconds)
tmin = 0.0
tmax = 50.0
# Average potassium channel conductance per unit area (mS/cm^2)
gK = 36.0
# Average sodoum channel conductance per unit area (mS/cm^2)
gNa = 120.0
# Average leak channel conductance per unit area (mS/cm^2)
gL = 0.3
# Membrane capacitance per unit area (uF/cm^2)
Cm = 1.0
# Potassium potential (mV)
VK = -12.0
# Sodium potential (mV)
VNa = 115.0
# Leak potential (mV)
Vl = 10.613
# Time values
T = np.linspace(tmin, tmax, 10000)
# Potassium ion-channel rate functions
def alpha_n(Vm):
return (0.01 * (10.0 - Vm)) / (np.exp(1.0 - (0.1 * Vm)) - 1.0)
def beta_n(Vm):
return 0.125 * np.exp(-Vm / 80.0)
# Sodium ion-channel rate functions
def alpha_m(Vm):
return (0.1 * (25.0 - Vm)) / (np.exp(2.5 - (0.1 * Vm)) - 1.0)
def beta_m(Vm):
return 4.0 * np.exp(-Vm / 18.0)
def alpha_h(Vm):
return 0.07 * np.exp(-Vm / 20.0)
def beta_h(Vm):
return 1.0 / (np.exp(3.0 - (0.1 * Vm)) + 1.0)
# n, m, and h steady-state values
def n_inf(Vm=0.0):
return alpha_n(Vm) / (alpha_n(Vm) + beta_n(Vm))
def m_inf(Vm=0.0):
return alpha_m(Vm) / (alpha_m(Vm) + beta_m(Vm))
def h_inf(Vm=0.0):
return alpha_h(Vm) / (alpha_h(Vm) + beta_h(Vm))
# Input stimulus
def Id(t):
if 0.0 < t < 1.0:
return 150.0
elif 10.0 < t < 11.0:
return 50.0
return 0.0
# Compute derivatives
def compute_derivatives(y, t0):
dy = np.zeros((4,))
Vm = y[0]
n = y[1]
m = y[2]
h = y[3]
# dVm/dt
GK = (gK / Cm) * np.power(n, 4.0)
GNa = (gNa / Cm) * np.power(m, 3.0) * h
GL = gL / Cm
dy[0] = (Id(t0) / Cm) - (GK * (Vm - VK)) - (GNa * (Vm - VNa)) - (GL * (Vm - Vl))
# dn/dt
dy[1] = (alpha_n(Vm) * (1.0 - n)) - (beta_n(Vm) * n)
# dm/dt
dy[2] = (alpha_m(Vm) * (1.0 - m)) - (beta_m(Vm) * m)
# dh/dt
dy[3] = (alpha_h(Vm) * (1.0 - h)) - (beta_h(Vm) * h)
return dy
# State (Vm, n, m, h)
Y = np.array([0.0, n_inf(), m_inf(), h_inf()])
# Solve ODE system
# Vy = (Vm[t0:tmax], n[t0:tmax], m[t0:tmax], h[t0:tmax])
Vy = odeint(compute_derivatives, Y, T)
References
-
- Hodgkin, A. L., Huxley, A. F., (1952), A quantitative description of membrane current and its application to conduction and excitation in nerve. The Journal of Physiology, 117 doi: 10.1113/jphysiol.1952.sp004764
In particular, for further details about biologically-inspired models, check this book:
-
- Abbott L. F., Dayan P., Theoretical Neuroscience: Computational and Mathematical Modeling of Neural Systems, The MIT Press, 2005
If you like this post, you can always donate to support my activity! One coffee is enough! And don’t forget to subscribe to my weekly newsletter!

