Il modello Hodgkin-Huxley (pubblicato nel 1952 su The Journal of Physiology [1]) è il più famoso modello di neuroni spike (anche se esistono alternative più semplici, come il modello “Integrate-and-fire”, che funziona abbastanza bene).
È costituito da un sistema di quattro equazioni differenziali ordinarie che possono essere facilmente integrate utilizzando diversi strumenti. L’idea principale si basa su una rappresentazione elettrica del neurone, considerando solo i canali ionici voltaggio-gettati del Potassio (K) e del Sodio (Na) (anche se possono essere estesi per includere altri canali). Una rappresentazione schematica è riportata nella figura seguente:
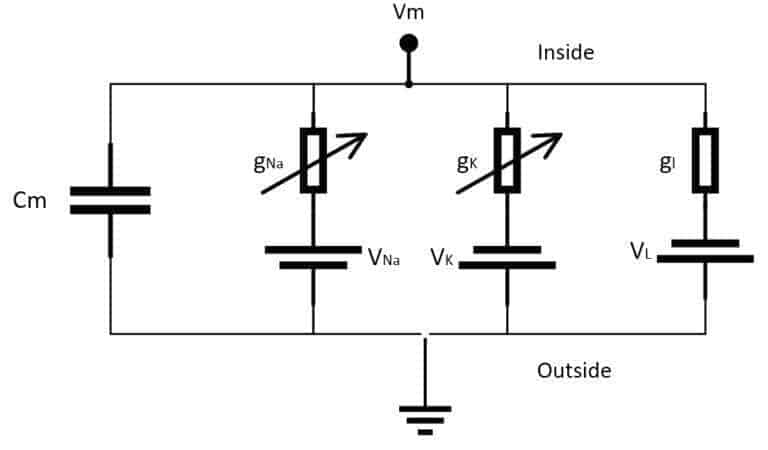
Gli elementi sono:
-
- Cm: una capacità per unità di superficie che rappresenta lo strato lipidico della membrana (valore adottato: 1 µF/cm²).
- gNa: conduttanza controllata dal voltaggio per unità di area associata al canale ionico del sodio (Na) (valore adottato: 120 µS/cm²)
- gK: conduttanza controllata dal voltaggio per unità di superficie associata al canale ionico del potassio (K) (valore adottato: 36 µS/cm²)
- gl: conduttanza per unità di superficie associata ai canali di perdita (valore adottato: 0,3 36 µS/cm²)
- VNa: fonte di tensione che rappresenta il gradiente elettrochimico per gli ioni sodio (valore adottato: 115 mV).
- VK: fonte di tensione che rappresenta il gradiente elettrochimico per gli ioni potassio (valore adottato: -12 mV).
- Vl: sorgente di tensione che determina la densità di corrente di dispersione insieme a gl (valore adottato: 10,613 mV)
Nello schema, la corrente di stimolo esterna non è mostrata, tuttavia, ne ipotizziamo la presenza come densità di corrente (I) che codifica il segnale di ingresso. Tutti i valori sperimentali sono gli stessi proposti dagli autori in [1] e si riferiscono a un potenziale di equilibrio di 0 V. Il sistema è definito attraverso il seguente sistema ODE:
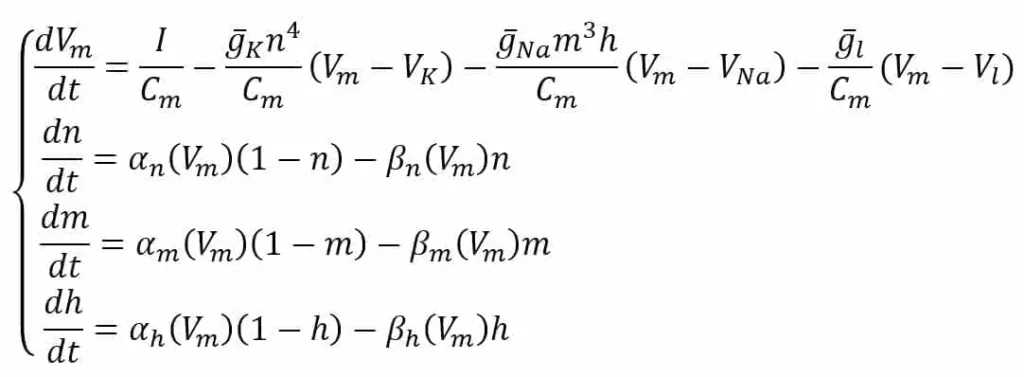
La prima equazione definisce la derivazione di Vm considerando lo stimolo esterno (I) e il contributo delle densità di corrente K, Na e di dispersione. Le variabili n, m e h sono associate alla probabilità di apertura di ciascun canale e dipendono strettamente dalla natura del canale. Per esempio, il canale K è voltaggio-gato e ha quattro subunità che devono essere tutte aperte per consentire il flusso di corrente, quindi la sua probabilità è n alla potenza di 4.
Il sodio ha un comportamento leggermente più complesso e necessita di due fattori diversi (m e h) con dinamiche autonome. Le ultime tre equazioni descrivono il modello cinetico del canale ionico, calcolando le derivate di n, m e h come funzioni delle stesse variabili e di due funzioni dipendenti dal voltaggio. Il primo termine è il numero di canali chiusi che si aprono, mentre il secondo termine è il numero di canali aperti che si chiudono.
Hodgkin e Huxley suggeriscono le seguenti funzioni:
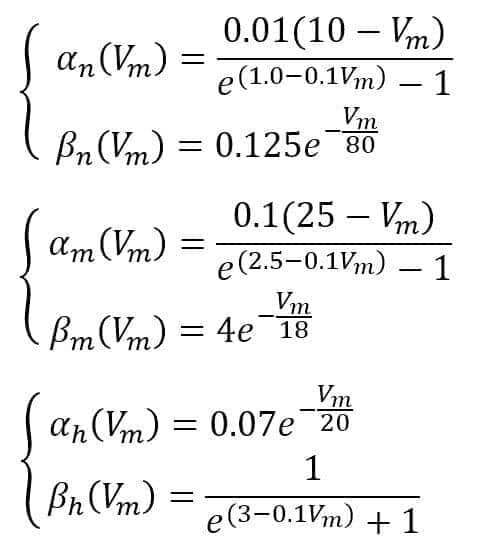
Nella simulazione, utilizzeremo una densità di corrente a doppio impulso come stimolo (tuttavia, qualsiasi altro segnale può essere utilizzato per testare diversi comportamenti). L’intervallo di tempo è [0, 50ms]:
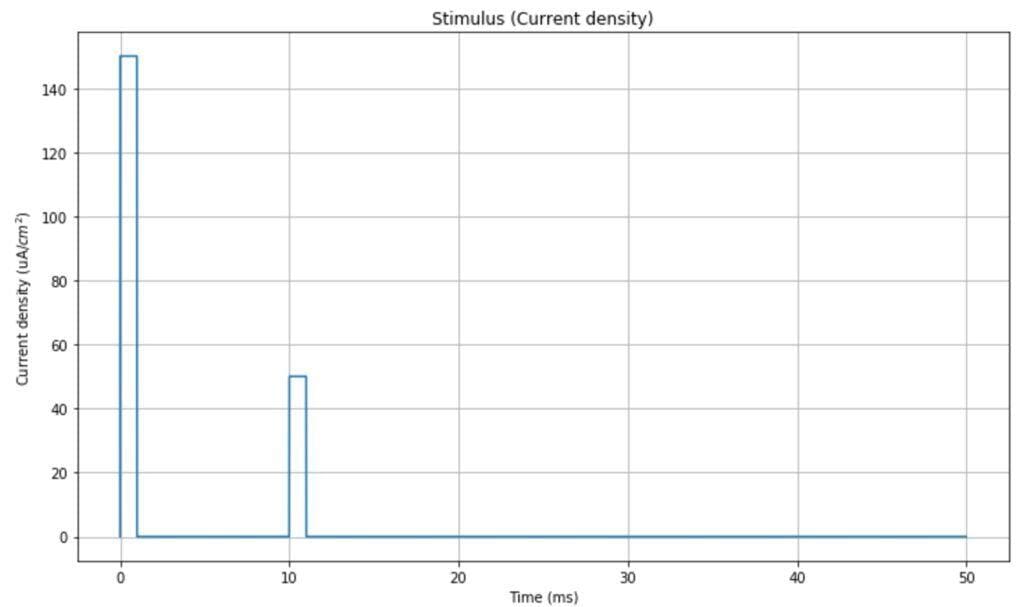
Il comportamento del neurone impulsivo risultante è mostrato nel seguente grafico:
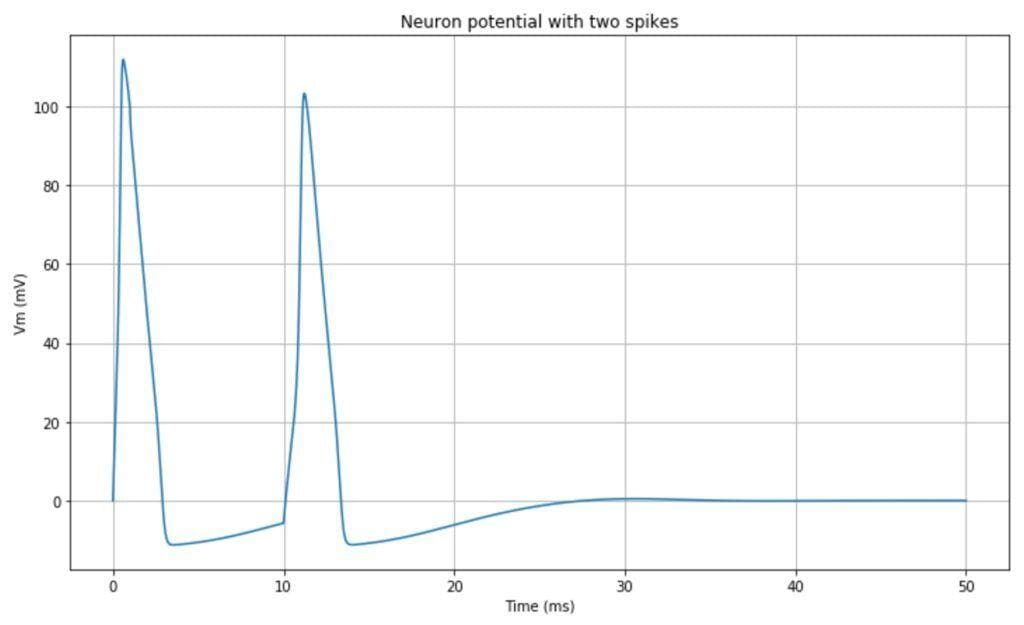
È anche possibile osservare i cicli limite presenti nel sistema dinamico. Nel grafico seguente, vengono tracciate le traiettorie Vm – n, e Vm – m:
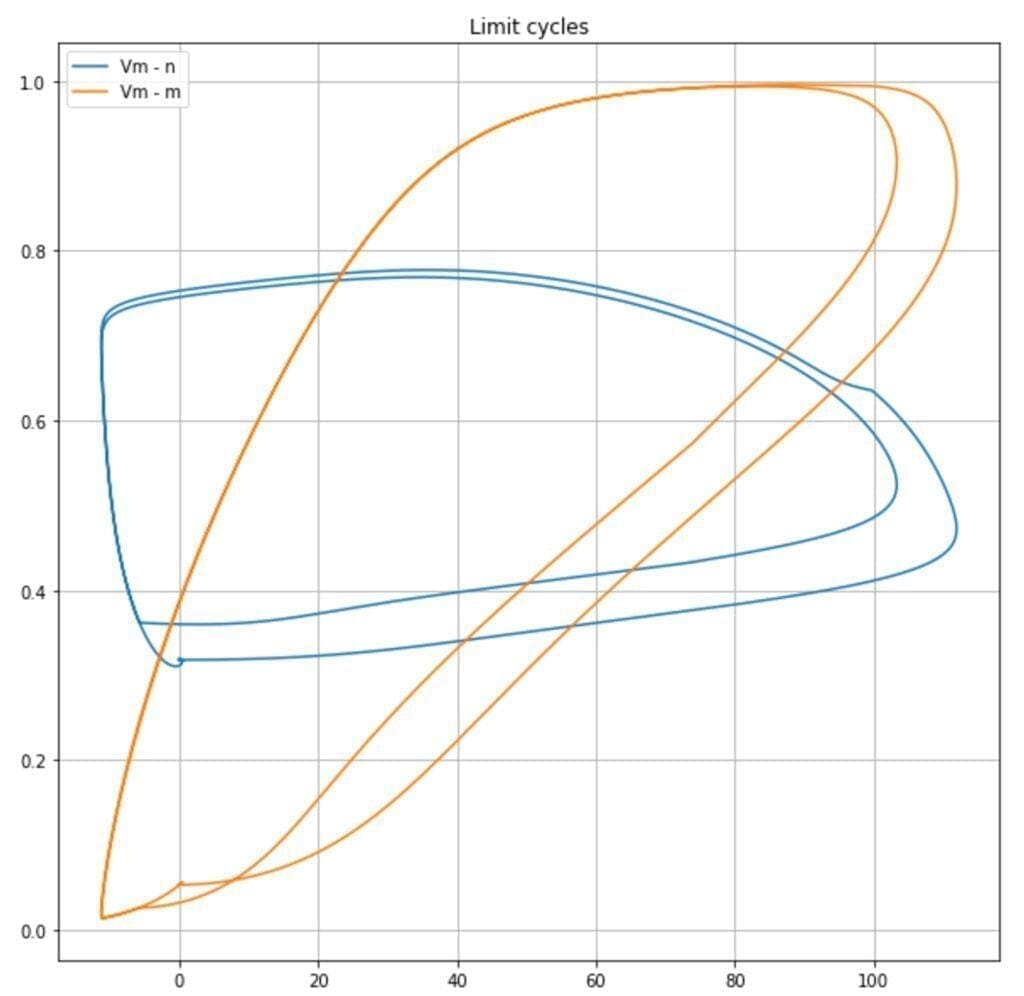
È possibile osservare come le probabilità (proporzionali a n, m e h) di apertura dei canali ionici vadano da un valore minimo a un valore massimo in base a n e Vm in modo ciclico. Questo permette le oscillazioni: stato stazionario, aumento del potenziale, picco, diminuzione del potenziale, stato stazionario.
Il codice Python completo è disponibile in questo GIST:
import matplotlib.pyplot as plt
import numpy as np
from scipy.integrate import odeint
# Set random seed (for reproducibility)
np.random.seed(1000)
# Start and end time (in milliseconds)
tmin = 0.0
tmax = 50.0
# Average potassium channel conductance per unit area (mS/cm^2)
gK = 36.0
# Average sodoum channel conductance per unit area (mS/cm^2)
gNa = 120.0
# Average leak channel conductance per unit area (mS/cm^2)
gL = 0.3
# Membrane capacitance per unit area (uF/cm^2)
Cm = 1.0
# Potassium potential (mV)
VK = -12.0
# Sodium potential (mV)
VNa = 115.0
# Leak potential (mV)
Vl = 10.613
# Time values
T = np.linspace(tmin, tmax, 10000)
# Potassium ion-channel rate functions
def alpha_n(Vm):
return (0.01 * (10.0 - Vm)) / (np.exp(1.0 - (0.1 * Vm)) - 1.0)
def beta_n(Vm):
return 0.125 * np.exp(-Vm / 80.0)
# Sodium ion-channel rate functions
def alpha_m(Vm):
return (0.1 * (25.0 - Vm)) / (np.exp(2.5 - (0.1 * Vm)) - 1.0)
def beta_m(Vm):
return 4.0 * np.exp(-Vm / 18.0)
def alpha_h(Vm):
return 0.07 * np.exp(-Vm / 20.0)
def beta_h(Vm):
return 1.0 / (np.exp(3.0 - (0.1 * Vm)) + 1.0)
# n, m, and h steady-state values
def n_inf(Vm=0.0):
return alpha_n(Vm) / (alpha_n(Vm) + beta_n(Vm))
def m_inf(Vm=0.0):
return alpha_m(Vm) / (alpha_m(Vm) + beta_m(Vm))
def h_inf(Vm=0.0):
return alpha_h(Vm) / (alpha_h(Vm) + beta_h(Vm))
# Input stimulus
def Id(t):
if 0.0 < t < 1.0:
return 150.0
elif 10.0 < t < 11.0:
return 50.0
return 0.0
# Compute derivatives
def compute_derivatives(y, t0):
dy = np.zeros((4,))
Vm = y[0]
n = y[1]
m = y[2]
h = y[3]
# dVm/dt
GK = (gK / Cm) * np.power(n, 4.0)
GNa = (gNa / Cm) * np.power(m, 3.0) * h
GL = gL / Cm
dy[0] = (Id(t0) / Cm) - (GK * (Vm - VK)) - (GNa * (Vm - VNa)) - (GL * (Vm - Vl))
# dn/dt
dy[1] = (alpha_n(Vm) * (1.0 - n)) - (beta_n(Vm) * n)
# dm/dt
dy[2] = (alpha_m(Vm) * (1.0 - m)) - (beta_m(Vm) * m)
# dh/dt
dy[3] = (alpha_h(Vm) * (1.0 - h)) - (beta_h(Vm) * h)
return dy
# State (Vm, n, m, h)
Y = np.array([0.0, n_inf(), m_inf(), h_inf()])
# Solve ODE system
# Vy = (Vm[t0:tmax], n[t0:tmax], m[t0:tmax], h[t0:tmax])
Vy = odeint(compute_derivatives, Y, T)
Riferimenti
-
- Hodgkin, A. L., Huxley, A. F., (1952), A quantitative description of membrane current and its application to conduction and excitation in nerve. The Journal of Physiology, 117 doi: 10.1113/jphysiol.1952.sp004764
In particolare, per ulteriori dettagli sui sistemi biologicamente-ispirati, suggerisco il libro:
-
- Abbott L. F., Dayan P., Theoretical Neuroscience: Computational and Mathematical Modeling of Neural Systems, The MIT Press, 2005
Se ti piace l’articolo, puoi sempre fare una donazione per supportare la mia attività. Basta un caffè! E non dimenticarti di iscriverti alla mia newsletter settimanale!

