La retropropagazione standard è probabilmente il miglior algoritmo di addestramento neurale per le reti poco profonde e profonde. Tuttavia, si basa sulla regola della catena delle derivate e un aggiornamento nei primi livelli richiede una conoscenza retroprodotta dall’ultimo livello. Questa non località, soprattutto nelle reti neurali profonde, riduce la plausibilità biologica del modello perché, anche se ci sono prove sufficienti di feedback negativo nei neuroni reali, è improbabile che, ad esempio, le sinapsi nel LGN (Nucleo Genicolato Laterale) possano cambiare le loro dinamiche (pesi) considerando una catena di cambiamenti a partire dalla corteccia visiva primaria. Inoltre, la back-propagation classica non si adatta molto bene alle reti di grandi dimensioni.
Per questi motivi, nel 1988, Fahlman ha proposto una regola di aggiornamento locale alternativa e più rapida, in cui la funzione di perdita totale L viene approssimata con una funzione polinomiale quadratica (utilizzando l’espansione di Taylor) per ogni peso in modo indipendente (supponendo che ogni aggiornamento abbia un’influenza limitata sui vicini). La regola di aggiornamento del peso risultante (che è un metodo del secondo ordine) è:
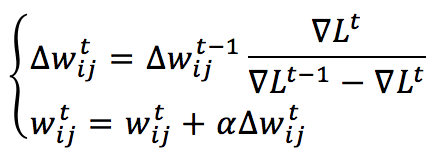
L è la funzione di costo (funzione di perdita totale) e il gradiente deve essere calcolato in base alla connessione tra il neurone i (appartenente a uno strato superiore) e il neurone j (appartenente a uno strato inferiore): ∇L(i,j), mentre alfa è il tasso di apprendimento. Questa regola è completamente locale (perché dipende solo dalle informazioni raccolte dalle unità pre e post-sinaptiche) e può anche essere molto veloce quando il problema è convesso ma, d’altra parte, presenta alcuni pesanti svantaggi:
-
- Deve memorizzare il gradiente precedente e la correzione del peso (questo è parzialmente plausibile dal punto di vista biologico).
- Può produrre salti ‘incerti’ quando la superficie di errore ha molti minimi locali a causa dell’approssimazione della funzione di perdita e della sua seconda derivata.
Per questi motivi, questo algoritmo è stato quasi abbandonato in favore della Retropropagazione che, insieme agli ottimizzatori più comuni, come RMSProp o Adam, può raggiungere la convergenza in reti molto profonde senza particolari inconvenienti.
Per testare Quickprop, ho implementato una rete neurale molto semplice (in realtà una Regressione Logistica):
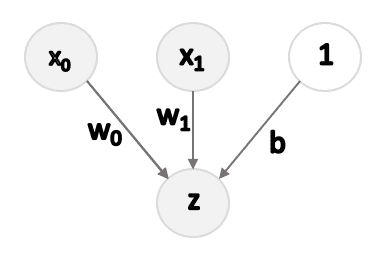
Per semplicità, il set di dati X è stato trasformato in una matrice (N, 3), con la terza colonna uguale a 1. In questo modo, il pregiudizio può essere appreso come qualsiasi altro peso. La funzione di costo basata sull’entropia incrociata è:
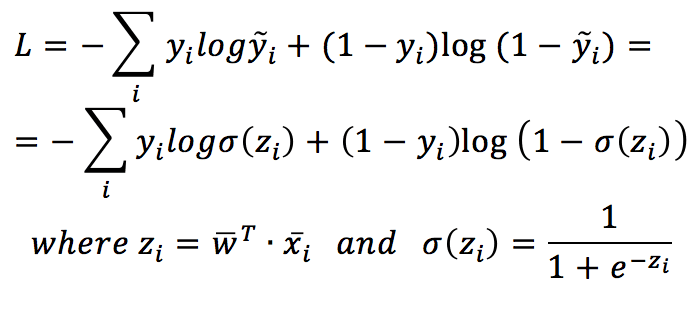
Il gradiente generico (in questo caso, ho considerato solo un indice singolo, perché c’è un solo strato) è:
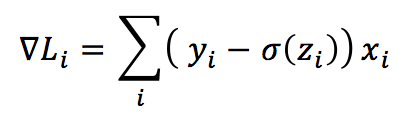
Il codice completo è disponibile anche nel GIST:
from sklearn.datasets import make_classification
import numpy as np
# Set random seed (for reproducibility)
np.random.seed(1000)
def sigmoid(arg):
return 1.0 / (1.0 + np.exp(-arg))
# Create random dataset
nb_samples = 500
nb_features = 2
X, Y = make_classification(n_samples=nb_samples,
n_features=nb_features,
n_informative=nb_features,
n_redundant=0,
random_state=4)
# Prepreprocess the dataset
Xt = np.ones(shape=(nb_samples, nb_features+1))
Xt[:, 0:2] = X
Yt = Y.reshape((nb_samples, 1))
# Initial values
W = np.random.uniform(-0.01, 0.01, size=(1, nb_features+1))
dL = np.zeros((1, nb_features + 1))
dL_prev = np.random.uniform(-0.001, 0.001, size=(1, nb_features + 1))
dW_prec = np.ones((1, nb_features + 1))
W_prev = np.zeros((1, nb_features + 1))
learning_rate = 0.0001
tolerance = 1e-6
# Run a training process
i = 0
while np.linalg.norm(W_prev - W, ord=1) > tolerance:
i += 1
sZ = sigmoid(np.dot(Xt, W.T))
dL = np.sum((Yt - sZ) * Xt, axis=0)
delta = dL / (dL_prev - dL)
dL_prev = dL.copy()
dW = dW_prec * delta
dW_prec = dW.copy()
W_prev = W.copy()
W += learning_rate * dW
print('Converged after {} iterations'.format(i))
La complessità è molto limitata, ma è possibile vedere che Quickprop può convergere molto rapidamente. In caso di oscillazioni, è meglio ridurre il tasso di apprendimento (questo rallenta anche la velocità complessiva). Tuttavia, in generale, per ogni problema in cui deve essere impiegato Quickprop, è utile trovare gli iperparametri ottimali (tasso di apprendimento e numero di iterazioni).
Per ulteriori dettagli:
-
- Fahlman S. E., An Empirical Study of Learning Speed in Back-Propagation Networks
- Rojas R., Neural Networks: A Systematic Introduction, Springer
Se ti piace l’articolo, puoi sempre fare una donazione per supportare la mia attività. Basta un caffè!

