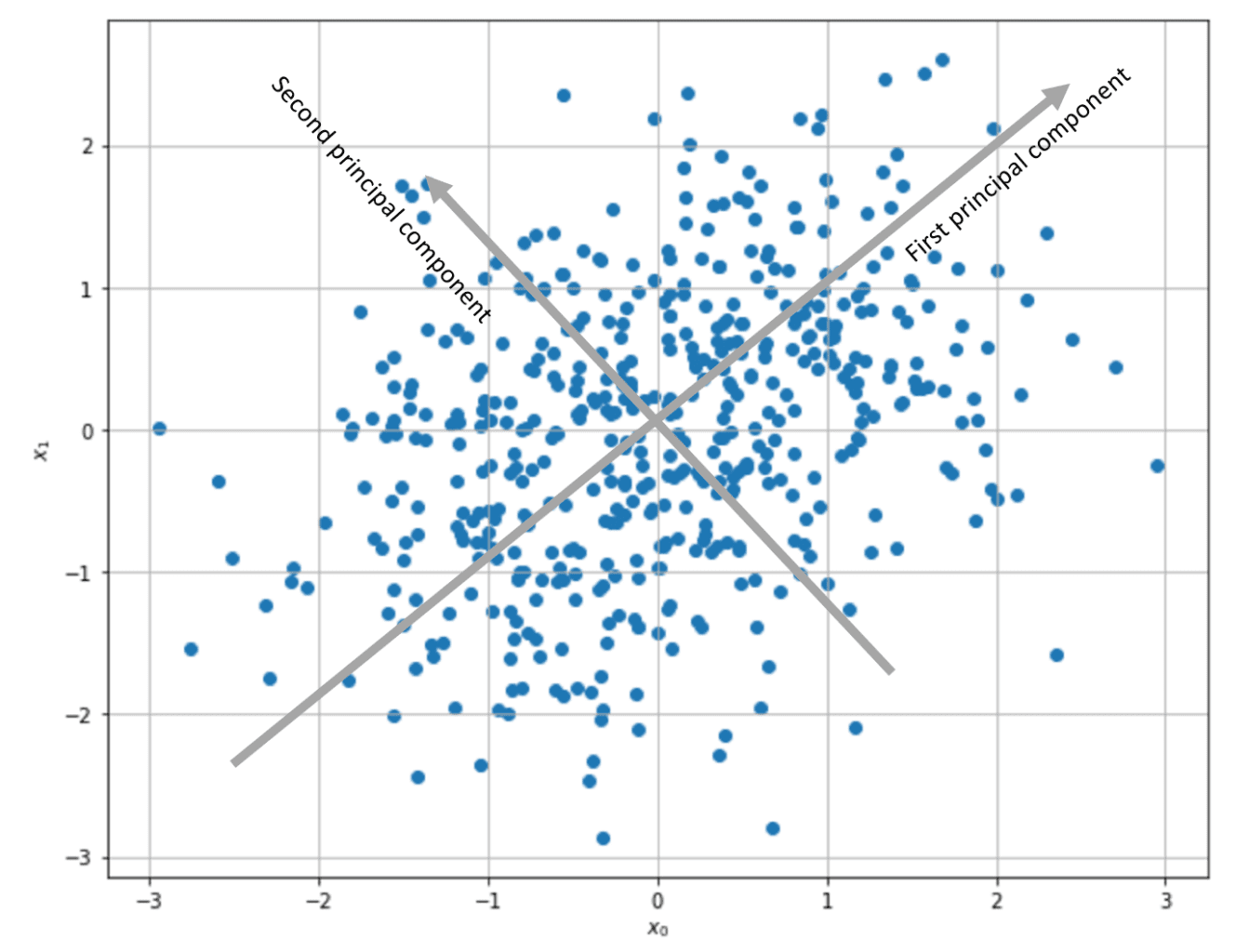
L’apprendimento hebbiano è una delle teorie di apprendimento più famose. È stata proposta dallo psicologo canadese Donald Hebb nel 1949, molti anni prima che i suoi risultati fossero confermati da esperimenti neuroscientifici. I ricercatori di Intelligenza Artificiale hanno capito subito l’importanza della sua teoria applicata alle reti neurali artificiali, e anche se sono stati adottati algoritmi più efficienti per risolvere problemi complessi, le neuroscienze continuano a trovare sempre più prove di neuroni naturali il cui processo di apprendimento è quasi perfettamente modellato dalle equazioni di Hebb.
La regola di Hebb è molto semplice e può essere discussa partendo da una struttura di alto livello di un neurone con una singola uscita:
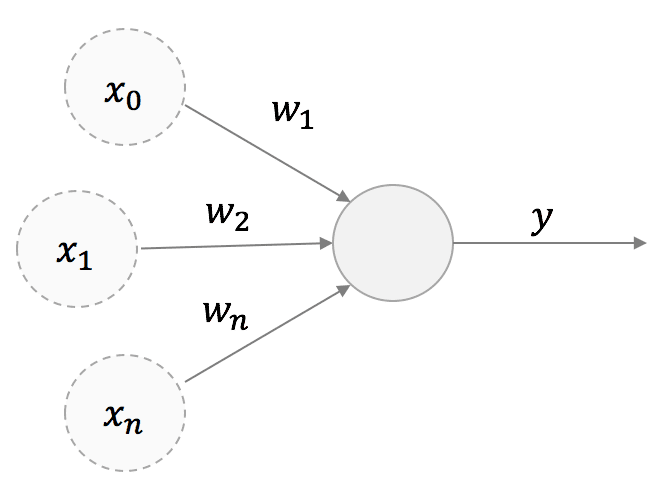
Stiamo considerando un neurone lineare; pertanto, l’uscita y è una combinazione lineare dei suoi valori di ingresso x:
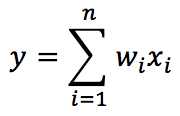
Secondo la teoria Hebbian, il peso sinaptico corrispondente sarà rinforzato se entrambe le unità pre e post-sinaptiche si comportano in modo simile (sparando o rimanendo ferme). D’altra parte, se il loro comportamento è discordante, saremo indeboliti. In altre parole, usando un famoso aforisma, “I neuroni che sparano insieme, si collegano insieme”. Da un punto di vista matematico, questa regola può essere espressa (in una versione discretizzata) come:
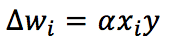
Alpha è il tasso di apprendimento. Per comprendere meglio le implicazioni di questa regola, è utile esprimerla utilizzando i vettori:
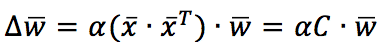
C è la matrice di correlazione dell’ingresso (se i campioni sono centrati su zero, C è anche la matrice di covarianza). Pertanto, il vettore dei pesi sarà aggiornato per massimizzare i componenti corrispondenti alla direzione della varianza massima dell’ingresso. In particolare, considerando la versione continua nel tempo, se C ha un autovalore dominante, la soluzione w(t) può essere espressa come un vettore con la stessa direzione dell’autovalore C corrispondente. In altre parole, l’apprendimento Hebbian esegue una PCA, estraendo la prima componente principale.
Anche se questo approccio è fattibile, questa regola ha un problema: è instabile. C è una matrice semidefinita positiva. Pertanto, i suoi autovalori sono sempre non negativi. Ciò significa che w(t) sarà una combinazione lineare di autovalori con coefficienti che aumentano esponenzialmente con t. Considerando la versione discreta, è facile capire che se x e y sono maggiori di 1, il processo di apprendimento aumenterà indefinitamente il valore assoluto dei pesi, producendo un overflow.
Questo problema può essere risolto imponendo la normalizzazione dei pesi dopo ogni aggiornamento (in modo da farli saturare a valori finiti). Tuttavia, questa soluzione è biologicamente improbabile, perché ogni sinapsi deve conoscere tutti gli altri pesi. Oja ha proposto l’approccio alternativo migliore, e la regola prende il suo nome:
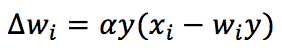
La regola è sempre Hebbian, ma ora include un termine auto-normalizzante (-wy²). È facile dimostrare che la corrispondente equazione differenziale continua nel tempo ha ora autovalori negativi e la soluzione w(t) converge. Proprio come nella regola di Hebb pura, il vettore w convergerà sempre all’autovettore C dominante, ma in questo caso la sua norma sarà un numero finito (piccolo).
Implementare la regola di Oja in Python (anche con Tensorflow) è molto semplice. Iniziamo con un set di dati bidimensionali casuali centrati (ottenuti utilizzando Scikit-Learn make_blobs() e StandardScaler()):
Nel GIST seguente, viene calcolata la matrice di covarianza (correlazione), insieme ai suoi autovalori, e poi viene applicata la regola di Oja al set di dati:
import numpy as np
from sklearn.datasets import make_blobs
from sklearn.preprocessing import StandardScaler
# Set random seed for reproducibility
np.random.seed(1000)
# Create and scale dataset
X, _ = make_blobs(n_samples=500, centers=2, cluster_std=5.0, random_state=1000)
scaler = StandardScaler(with_std=False)
Xs = scaler.fit_transform(X)
# Compute eigenvalues and eigenvectors
Q = np.cov(Xs.T)
eigu, eigv = np.linalg.eig(Q)
# Apply the Oja's rule
W_oja = np.random.normal(scale=0.25, size=(2, 1))
prev_W_oja = np.ones((2, 1))
learning_rate = 0.0001
tolerance = 1e-8
while np.linalg.norm(prev_W_oja - W_oja) > tolerance:
prev_W_oja = W_oja.copy()
Ys = np.dot(Xs, W_oja)
W_oja += learning_rate * np.sum(Ys*Xs - np.square(Ys)*W_oja.T, axis=0).reshape((2, 1))
# Eigenvalues print(eigu) [ 0.67152209 1.33248593] # Eigenvectors print(eigv) [[-0.70710678 -0.70710678] [ 0.70710678 -0.70710678]] # W_oja at the end of the training process print(W_oja) [[-0.70710658] [-0.70710699]]
Come si può vedere, l’algoritmo ha convergenza sul secondo autovalore, il cui autovalore corrispondente è il più alto.
Un’estensione della regola di Oja alle reti multi-uscita è fornita dalla regola di Sanger (nota anche come Algoritmo Hebbiano Generalizzato):
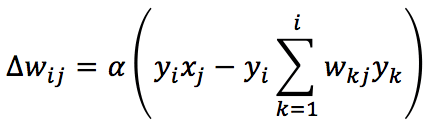
In questo caso, il fattore di normalizzazione (e di decorrelazione) viene applicato considerando solo i pesi sinaptici precedenti a quello attuale (incluso). Utilizzando una notazione vettoriale, la regola di aggiornamento diventa:
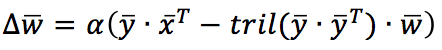
Tril() è una funzione che restituisce il triangolo inferiore di una matrice quadrata. La regola di Sanger è in grado di estrarre tutte le componenti principali, partendo dalla prima e continuando con tutte le unità di uscita. Come per la regola di Oja, nel GIST seguente, la regola viene applicata allo stesso set di dati:
import numpy as np
from sklearn.datasets import make_blobs
from sklearn.preprocessing import StandardScaler
# Set random seed for reproducibility
np.random.seed(1000)
# Create and scale dataset
X, _ = make_blobs(n_samples=500, centers=2, cluster_std=5.0, random_state=1000)
scaler = StandardScaler(with_std=False)
Xs = scaler.fit_transform(X)
# Compute eigenvalues and eigenvectors
Q = np.cov(Xs.T)
eigu, eigv = np.linalg.eig(Q)
W_sanger = np.random.normal(scale=0.1, size=(2, 2))
prev_W_sanger = np.ones((2, 2))
learning_rate = 0.1
nb_iterations = 2000
t = 0.0
for i in range(nb_iterations):
prev_W_sanger = W_sanger.copy()
dw = np.zeros((2, 2))
t += 1.0
for j in range(Xs.shape[0]):
Ysj = np.dot(W_sanger, Xs[j]).reshape((2, 1))
QYd = np.tril(np.dot(Ysj, Ysj.T))
dw += np.dot(Ysj, Xs[j].reshape((1, 2))) - np.dot(QYd, W_sanger)
W_sanger += (learning_rate / t) * dw
W_sanger /= np.linalg.norm(W_sanger, axis=1).reshape((2, 1))
# Eigenvalues print(eigu) [ 0.67152209 1.33248593] # Eigenvectors print(eigv) [[-0.70710678 -0.70710678] [ 0.70710678 -0.70710678]] # W_sanger at the end of the training process print(W_sanger) [[-0.72730535 -0.69957863] [-0.67330094 0.72730532]]
Come si può vedere, la matrice dei pesi contiene (come colonne) le due componenti principali (approssimativamente parallele agli autovalori di C).
Grazie alla sua semplicità e all’evidenza biologica, l’apprendimento hebbiano è un approccio molto potente e non supervisionato. Applicare questa metodologia a problemi bio-ispirati come la sensibilità all’orientamento è facile. Raccomando [1] per ulteriori dettagli su queste tecniche e altri modelli neuroscientifici.
Riferimenti:
-
- Dayan P., Abbott L. F., Theoretical Neuroscience: Computational and Mathematical Modeling of Neural Systems, The MIT Press
Se ti piace l’articolo, puoi sempre fare una donazione per supportare la mia attività. Basta un caffè!