A differenza della maggior parte degli algoritmi di apprendimento automatico, l’Apprendimento Basato sulle Istanze è privo di modelli, il che significa che non ci sono forti assunzioni sulla struttura dei regressori, dei classificatori o delle funzioni di clustering. Sono ‘semplicemente’ determinati dai dati, secondo un’affinità indotta da una metrica di distanza (il nome più comune per questo approccio è Vicini più vicini).
Se abbiamo un set di dati X:
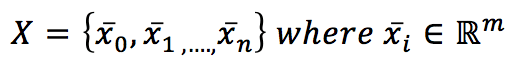
è possibile introdurre una metrica nell’iperspazio m-dimensionale. La scelta più comune è la metrica euclidea:
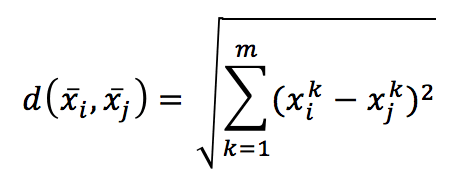
Calcolando la distanza tra ogni coppia di campioni, otteniamo una matrice simmetrica, che è già una misura globale dell’affinità tra i punti:
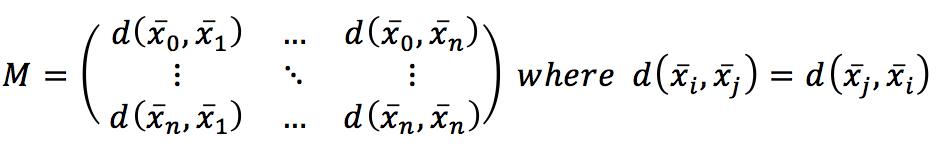
In effetti, anche se non si tratta di un modello, è la cosa più simile a un modello basato sulla struttura naturale dei dati di formazione. Considerando che l’iperspazio è normalmente uno spazio di caratteristiche; due punti vicini condividono (o hanno caratteristiche simili). Questo è l’unico presupposto reale in questo tipo di approccio e, di fatto, la geometria del set di dati (insieme a una funzione di distanza) è l’algoritmo stesso. Pertanto, la previsione viene fatta cercando i primi k vicini più vicini e:
-
- In un approccio di clustering, li consideriamo come un insieme di oggetti molto simili, le cui caratteristiche possono essere ereditate dal nuovo campione. Un’applicazione comune è quella dei sistemi di raccomandazione basati sull’utente, dove un nuovo utente deve ‘prendere in prestito’ le caratteristiche fornite dai suoi vicini.
- In un approccio di classificazione, facendo la media delle classi (è anche possibile ponderarle utilizzando le distanze normalizzate), è facile determinare la classe del nuovo campione.
- In un approccio di regressione, considerando il valore ponderato di tutti i vicini come punti di addestramento per una regressione standard
Purtroppo, il calcolo di M è molto costoso; con n campioni appartenenti a uno spazio m-dimensionale, dobbiamo calcolare m moltiplicazioni per ogni coppia di campioni. Ciò significa che questo algoritmo, spesso chiamato ‘forza bruta’, ha una complessità di ‘addestramento’ O(mn²) e una complessità di predizione O(mn), dimostrando di soffrire di una drammatica maledizione della dimensionalità.
Per superare questo problema, sono state proposte due alternative (e sono tutte implementate da Scikit-Learn):
-
- KD-Alberi
- Alberi a sfera
Un albero KD è un’estensione naturale di un albero binario a dati K-dimensionali. L’idea è piuttosto semplice e può essere spiegata considerando la figura seguente:
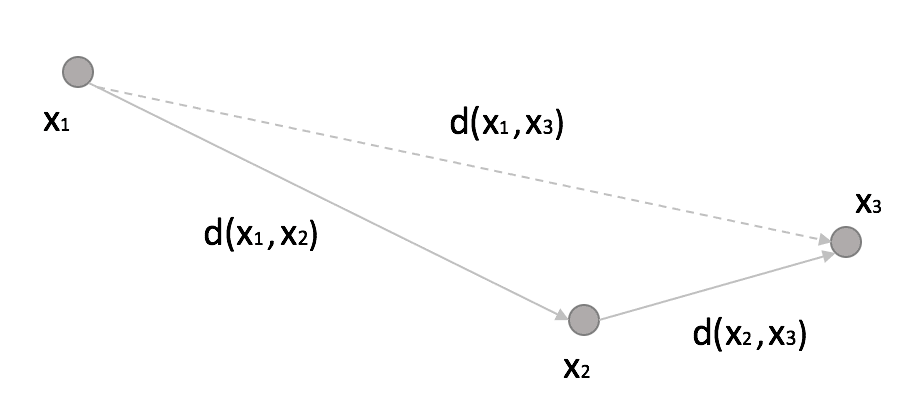
Se impostiamo una soglia R, allora:
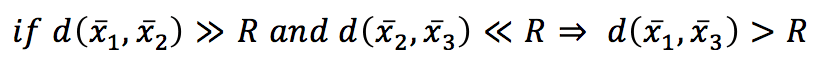
In altre parole, se la distanza tra x1 e x2 supera una soglia fissa (squalificando x2 dall’essere un vicino) e la distanza tra x2 e x3 è molto più breve di R, allora anche x3 è un non vicino e non ha senso calcolare la distanza tra x1 e x3 in modo esplicito. Con un KD-Tree, lo spazio viene suddiviso utilizzando nodi binari a k dimensioni e in ognuno di essi viene scelta una sola dimensione per dividere il sottospazio originale in due semispazi. La dinamica è molto intuitiva in 2D. Grazie ai collaboratori di Wikipedia KiwiSunset e MYguel, posso mostrare un semplice esempio senza dover ridisegnare da zero.
Ci sono 6 punti in uno spazio 2D:
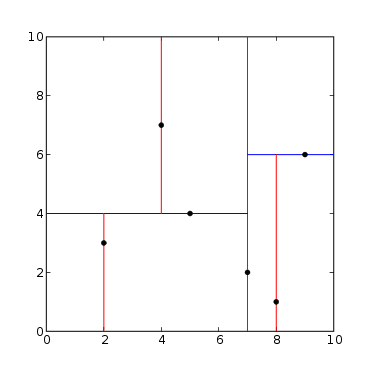
Le linee rosse rappresentano i tagli sull’asse X e le linee rosse sull’asse Y. Partendo dal punto (7, 2) e tagliando su X, abbiamo 3 punti dove x<7 e due punti dove x>7:
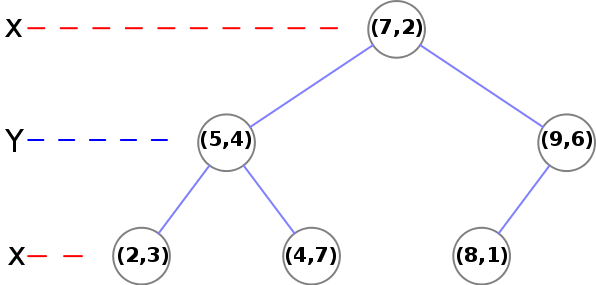
Al secondo livello, dobbiamo utilizzare Y:
-
- (5, 4) -> C’è un nodo (2, 3) dove y<4 e un altro nodo (4, 7) dove y>4
- (9, 6) -> C’è un nodo finale (foglia) (8, 1)
La procedura è semplice e può essere estesa a campioni k-dimensionali. Trattandosi di un albero binario, la complessità di formazione diventa O(mn log(n)). Anche se questo è un risultato migliore rispetto a un algoritmo di forza bruta, un KD-Tree non è in grado di sfruttare la struttura radiale della metrica euclidea ed è molto sensibile alla dimensionalità.
Ball-Tree rappresenta un algoritmo alternativo che spesso può superare KD-Tree. Un albero di sfere è sempre un albero binario, ma, in questo caso, ogni nodo definisce un’ipersfera, e due sotto-nodi definiscono due sotto-iper-sfere la cui unione deve contenere tutti i punti assegnati al nodo padre, e la cui intersezione è sempre vuota (anche se le ipersfere si sovrappongono). La dinamica non è molto diversa da quella degli alberi KD, ma in generale gli alberi a sfere sono più efficienti quando la dimensionalità è molto alta. Infatti, considerando uno scenario simile a quello presentato in precedenza, possiamo considerare un punto x1 (eventualmente un punto di predizione) e un altro punto x2 con un sottoalbero in cui troviamo x3 e x4:
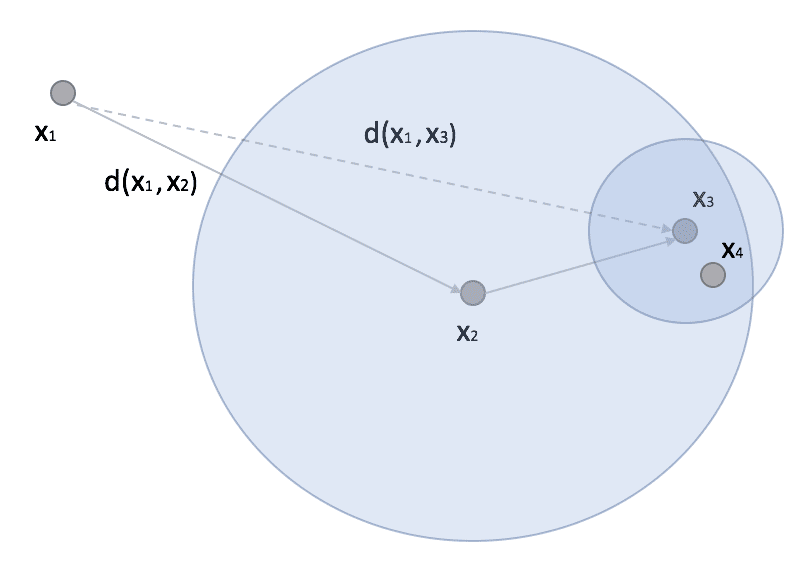
Nella ricerca, se x2 è il punto più vicino (a x1), tutti i punti appartenenti alla sfera il cui centroide ha una distanza da x1 maggiore di d(x1, x2) possono essere completamente scartati perché tutti i suoi punti sono più distanti di x2. Se la sfera è molto densa, riduce drasticamente il numero di confronti e le prestazioni complessive diventano superiori alla versione con KD-Tree.
Scikit-Learn implementa clustering, classificazione e regressione basati su algoritmi k-Nearest-Neighbors (con forza bruta, KD-Trees, Ball-Trees e diverse metriche). L’utilizzo è molto intuitivo e non c’è bisogno di fornire ulteriori esempi (sul sito web, ci sono molte applicazioni interessanti). Tuttavia, volevo confrontare le prestazioni di tutti gli algoritmi. Nel seguente frammento, vengono creati 10 set di dati (con un numero crescente di campioni e dimensioni) e viene inizializzata un’istanza NearestNeighbors per ogni coppia (set di dati, algoritmo):
from sklearn.datasets import make_blobs
from sklearn.neighbors import NearestNeighbors
import matplotlib.pyplot as plt
import multiprocessing
import numpy as np
import time
# Set random seed (for reproducibility)
np.random.seed(1000)
nb_samples = [50, 100, 500, 1000, 2000, 5000, 10000, 50000, 100000, 500000]
nb_features = [10, 25, 50, 75, 100, 150, 250, 300, 400, 500, 800, 1000, 2000]
algorithms = ['brute', 'kd_tree', 'ball_tree']
training_times = {'brute': [],
'kd_tree': [],
'ball_tree': []}
prediction_times = {'brute': [],
'kd_tree': [],
'ball_tree': []}
for i in range(len(nb_samples)):
for algorithm in algorithms:
X, _ = make_blobs(n_samples=nb_samples[i], n_features=nb_features[i],
centers=int(nb_features[i]/10), random_state=1000)
# Create k-Nearest Neighbors instance
nn = NearestNeighbors(algorithm=algorithm, n_jobs=multiprocessing.cpu_count())
# Training
start_time = time.time()
nn.fit(X)
end_time = time.time()
training_times[algorithm].append(end_time - start_time)
# Prediction
xs = np.random.uniform(-1.0, 1.0, size=nb_features[i])
start_time = time.time()
nn.kneighbors(xs.reshape(1, -1), n_neighbors=5)
end_time = time.time()
prediction_times[algorithm].append(end_time - start_time)
# Show the results
fig, ax = plt.subplots(6, 1, figsize=(12, 17))
# Training times
ax[0].set_title('Training time (Brute-force algorithm)')
ax[0].set_xlabel('Number of samples')
ax[0].set_ylabel('Time (seconds)')
ax[0].plot(nb_samples, training_times['brute'])
ax[0].grid()
ax[1].set_title('Training time (KD-Tree algorithm)')
ax[1].set_xlabel('Number of samples')
ax[1].set_ylabel('Time (seconds)')
ax[1].plot(nb_samples, training_times['kd_tree'])
ax[1].grid()
ax[2].set_title('Training time (Ball-Tree algorithm)')
ax[2].set_xlabel('Number of samples')
ax[2].set_ylabel('Time (seconds)')
ax[2].plot(nb_samples, training_times['ball_tree'])
ax[2].grid()
# Prediction times
ax[3].set_title('Prediction time (Brute-force algorithm)')
ax[3].set_xlabel('Number of samples')
ax[3].set_ylabel('Time (seconds)')
ax[3].plot(nb_samples, prediction_times['brute'])
ax[3].grid()
ax[4].set_title('Prediction time (KD-Tree algorithm)')
ax[4].set_xlabel('Number of samples')
ax[4].set_ylabel('Time (seconds)')
ax[4].plot(nb_samples, prediction_times['kd_tree'])
ax[4].grid()
ax[5].set_title('Prediction time (Ball-Tree algorithm)')
ax[5].set_xlabel('Number of samples')
ax[5].set_ylabel('Time (seconds)')
ax[5].plot(nb_samples, prediction_times['ball_tree'])
ax[5].grid()
plt.show()
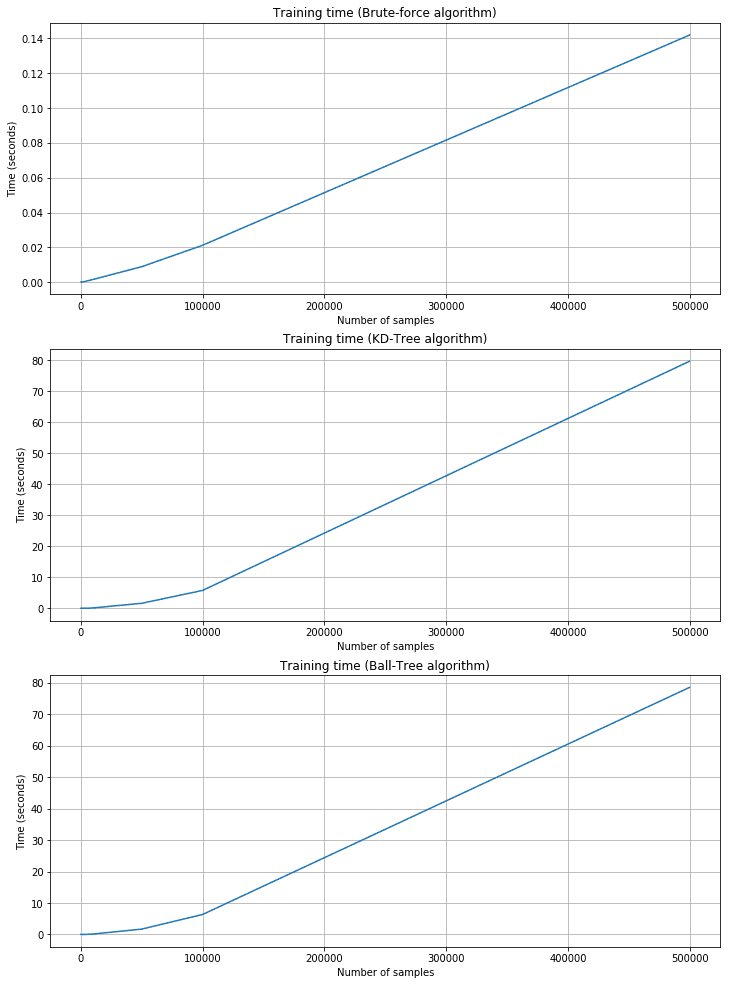
Grafici dei tempi di allenamento:
Grafici del tempo di previsione:
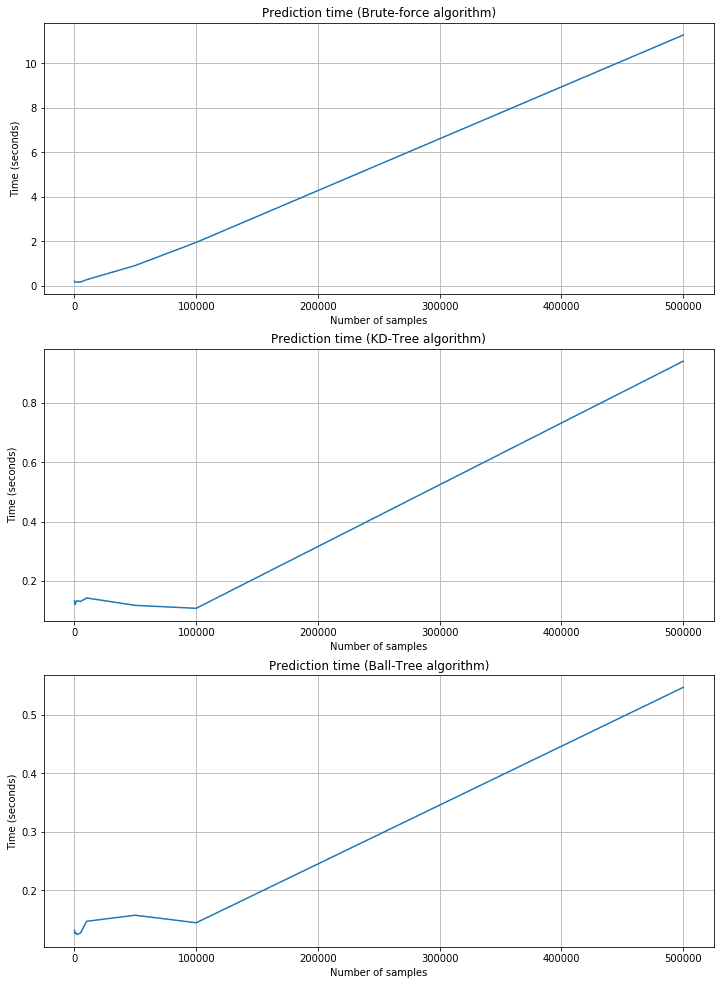
Come previsto, il tempo di addestramento è più breve per la forza bruta, ma il tempo di predizione corrispondente è più lungo. KD-Tree e Ball-Tree hanno tempi di formazione più lunghi a causa della necessità di costruire gli alberi. Tuttavia, le query sono molto veloci. Ad esempio, con 500.000 campioni a 2000 dimensioni, la forza bruta richiede circa 11 secondi, mentre KD-Tree è di circa 0,95 e Ball-Tree è di 0,55. Le prestazioni di forza bruta sono accettabili solo quando n e m sono molto piccoli e il costo della costruzione di un albero è troppo alto. In tutti questi casi, Scikit-Learn offre una quarta alternativa chiamata ‘auto’, che seleziona automaticamente la strategia migliore in base alla dimensionalità e utilizza ‘leaf_size’ per passare da un algoritmo ad albero a uno a forza bruta.
Se ti piace l’articolo, puoi sempre fare una donazione per supportare la mia attività. Basta un caffè!

