Model-free collaborative filtering is a “lightweight” approach to recommendation systems. It’s always based on the implicit “collaboration” (regarding ratings) among users. Still, it is computed in memory without using complex algorithms like ALS (Alternating Least Squares) that can be executed in a parallel environment (like Spark).
If we assume to have N users and M products, it’s possible to define a user-preference sparse matrix:
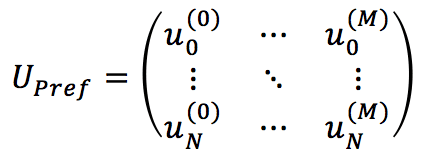
Each element represents the user’s rating of item j (0 means no rating has been provided). To face the differences belonging to many different contexts, it’s helpful to define two kinds of ratings (or feedback):
-
- Explicit feedback: an actual rating (like three stars or 8 out of 10)
- Implicit feedback: a page view, song play, move play, and so forth
The different kinds of feedback also determine the best metric to compare users. Once the user preference matrix has been populated, it’s necessary to compute the affinity matrix based on a similarity metric (the most common is the Euclidean one):
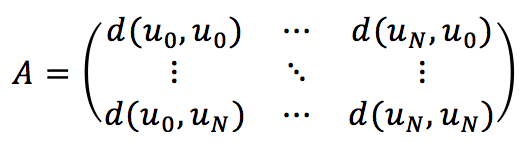
This matrix is built considering the rows of Upref. In particular, Upref[i] represents the preference vector (overall products) for the user i.
When the feedback is explicit, it can be helpful to keep using the Euclidean metric, but when it’s implicit, it can have a different meaning, and it can be better to pick another metric function. For example, if we use a binary encoding for the feedback (0 means no interaction and one single or multiple interactions), we could be interested in considering two users similar when they have the same amount of interactions (page views, song/movie plays, …). Therefore the Hamming distance can be more appropriate.
In this implementation, I’ve used Scikit-Learn to compute the pairwise distances, but other exciting solutions like Crab (http://muricoca.github.io/crab/). The source code is also available in this GIST.
from scipy.sparse import dok_matrix
from sklearn.metrics.pairwise import pairwise_distances
import numpy as np
# Set random seed (for reproducibility)
np.random.seed(1000)
# Create a dummy user-item dataset
nb_users = 1000
nb_products = 2500
max_rating = 5
max_rated_products = 500
X_preferences = dok_matrix((nb_users, nb_products), dtype=np.uint8)
for i in range(nb_users):
# Extract n random products
n_products = np.random.randint(0, max_rated_products+1)
products = np.random.randint(0, nb_products, size=n_products)
# Populate preference sparse matrix
for p in products:
X_preferences[i, p] = np.random.randint(0, max_rating+1)
# Compute pairwise distances
distance_matrix = pairwise_distances(X_preferences, metric='euclidean')
# Sort distances
sorted_distances = np.argsort(distance_matrix, axis=1)
test_user=500
# Take the top-10 simular users
for d in sorted_distances[test_user][::-1][0:10]:
print(d)
630 189 781 199 789 697 689 105 889 893
Once the list of top neighbors has been determined, it’s possible to suggest the top-k products, selecting them from the union of the most rated “neighbor” products:
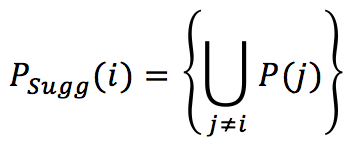
The predicted rating for a suggested item can be obtained as the weighted average of the neighborhood. For example, it’s possible to determine a weigh vector using a softmax function:
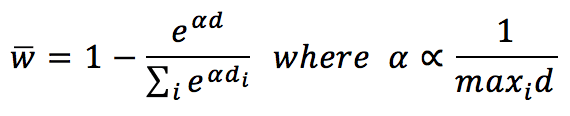
Alpha is a normalization parameter introduced to avoid an overflow with too large distances. The weight vector is referred to the subset of suggested items. The average rating is obtained as follows:
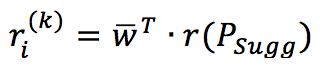
Of course, this is only possible when the reader can employ different techniques to compute the expected rating. For example, it’s possible to use a radial basis function with a low variance to penalize the contributions given by the most distant elements. At the same time, it’s possible to implement different affinities for the same task, evaluating the difference in the suggested products. A recommender isn’t seldom based on an “off-the-shelf” solution because of the intrinsic diversities in several business contexts. Therefore, I always suggest trying various alternatives before making the final decision.
If you like this post, you can always donate to support my activity! One coffee is enough!

